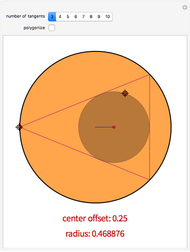
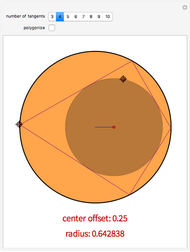
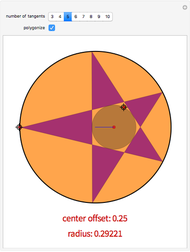
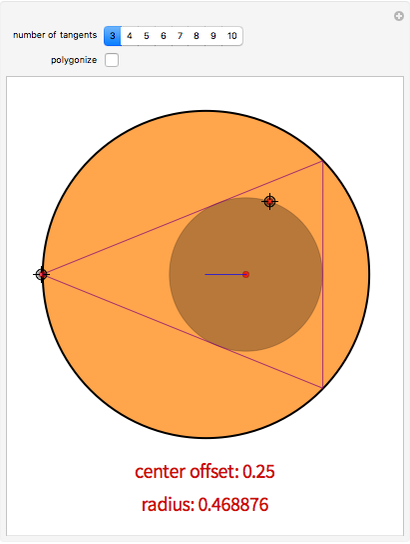
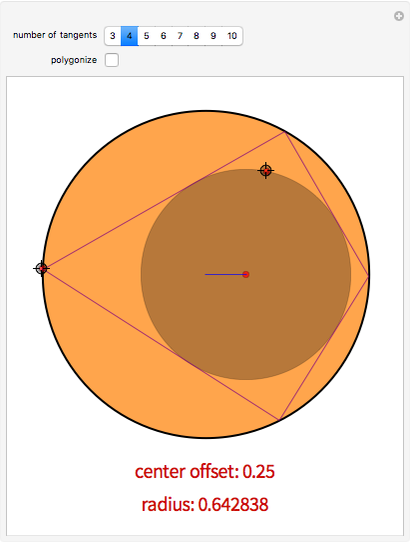
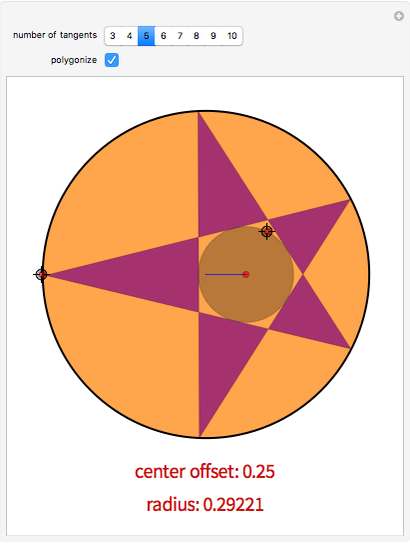
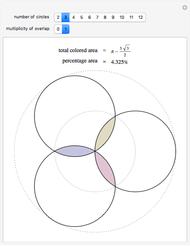
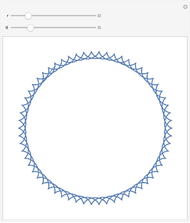
Given two nested circles, you can play the following game: choose a point on the outer circle
, draw the tangent to the inner circle
until it intersects
and continue repeatedly drawing tangents to
. You obtain a polygonal line inscribed in
and circumscribed about
called a Poncelet transverse.
Suppose that the aim of the game is to make this polygonal line meet the starting point. The Poncelet closure theorem states that if the polygonal line closes, then starting at any other point will also result in a closed polygonal line.
In this Demonstration you can use handles to change the center offset of
(separation between the centers of
and
) and its radius, whose current values will appear below the figure. You can also move the starting point and, when done, polygonize the final polygon.
Explicit formulas for the radius given the center offset are known only for the cases of three and four tangents; higher cases involve elliptic functions.
Press Alt to move a handle in smaller steps to increase precision.
Browse all topics
