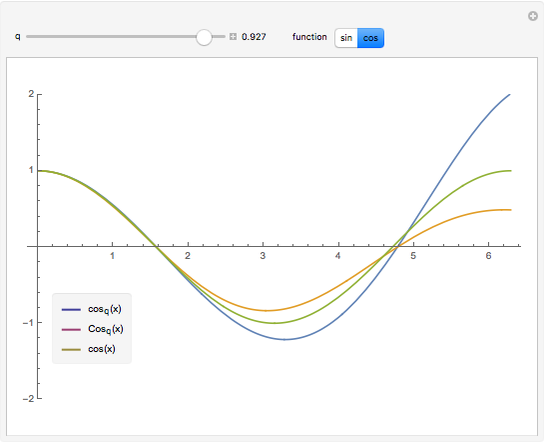
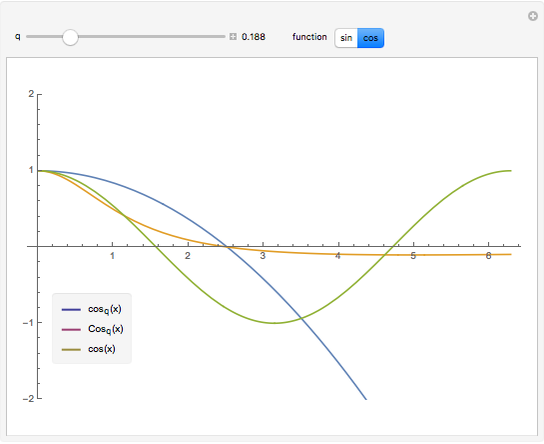
q-Trigonometric Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
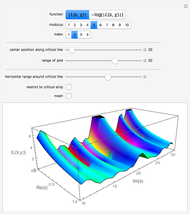
The  -analogs of trigonometric functions are built out of
-analogs of trigonometric functions are built out of  -exponentials in the same way that the classical trigonometric functions are built out of the classical exponential function. The existence of two flavors of
-exponentials in the same way that the classical trigonometric functions are built out of the classical exponential function. The existence of two flavors of  -exponents makes for two kinds of
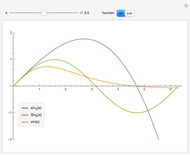
-exponents makes for two kinds of  -trigonometric functions:
-trigonometric functions: 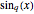 and
and 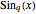 for
for 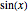 and
and 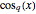 and
and 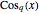 for
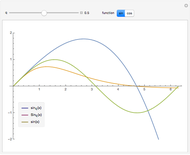
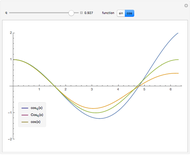
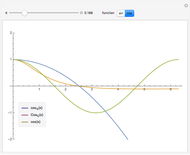
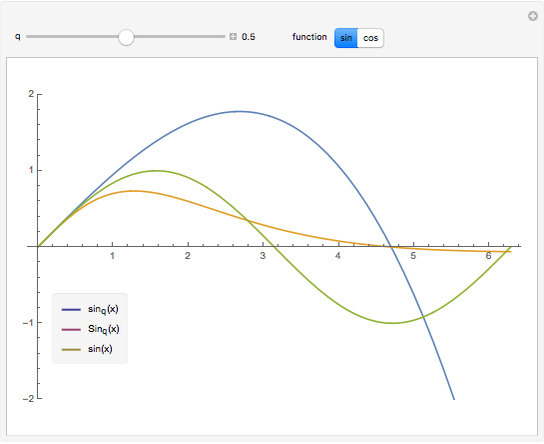
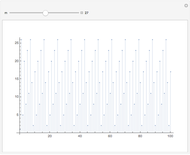
for 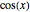 . These triples are plotted for various
. These triples are plotted for various 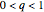 on the interval
on the interval 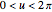 . You can see how the
. You can see how the  -analogs approach their classical counterparts as
-analogs approach their classical counterparts as  tends to 1.
tends to 1.
Contributed by: Oleksandr Pavlyk (March 2011)
Open content licensed under CC BY-NC-SA
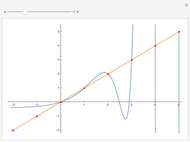
Snapshots
Details
The  -sine and
-sine and  -cosine functions can also be defined by the following series:
-cosine functions can also be defined by the following series:
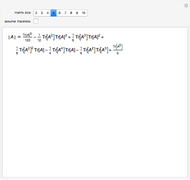
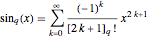 ;
;
 ;
;
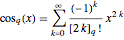 ;
;
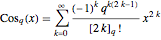 .
.
The  -sine and
-sine and  -cosine functions have
-cosine functions have  -analogs of the defining algebraic identity satisfied by their classical counterparts:
-analogs of the defining algebraic identity satisfied by their classical counterparts: 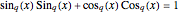 . Additionally they satisfy
. Additionally they satisfy  .
.
V. Kac and P. Cheung, Quantum Calculus, New York: Springer, 2001.
Permanent Citation