Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Determinant Using Traces

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

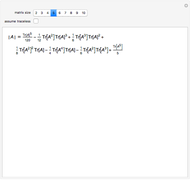
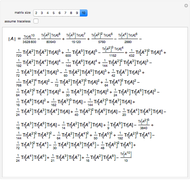
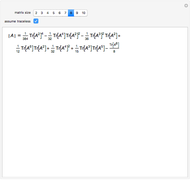
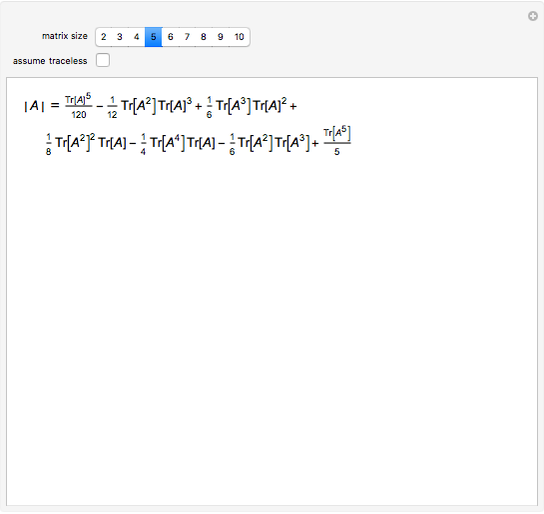
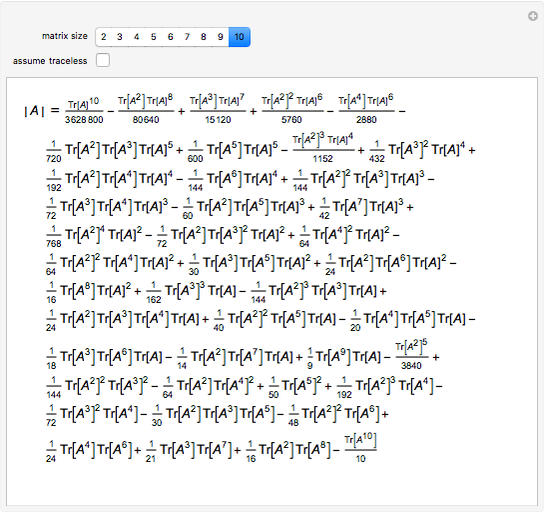
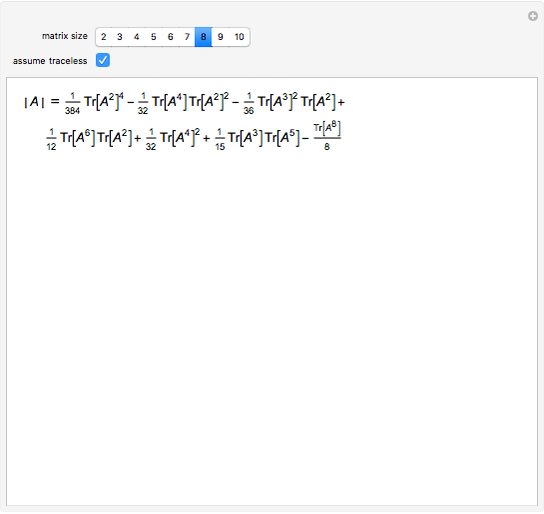
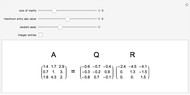
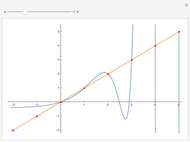
The determinant of a square matrix can be computed as a polynomial of traces of the matrix and its powers. This expression greatly simplifies for traceless matrices.

Contributed by: Oleksandr Pavlyk (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Consider the polynomial in of degree , where is the identity matrix. Its leading coefficient is .

On the other hand,

.

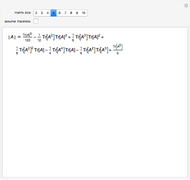
Comparing coefficients in the powers of λ gives .

This derivation is due to Vladimir Dudchenko, the first prize winner of the Russian StudentMathematicaContest.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send