Quantum Harmonic Oscillator Tunneling into Classically Forbidden Regions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
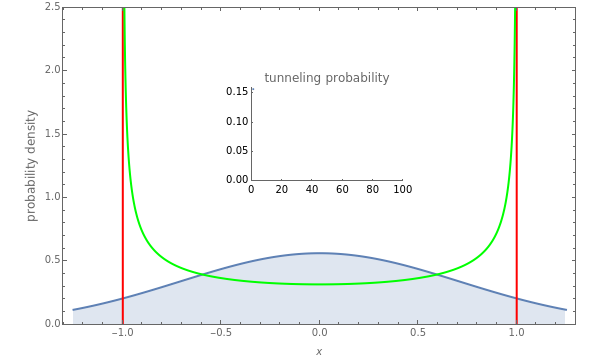
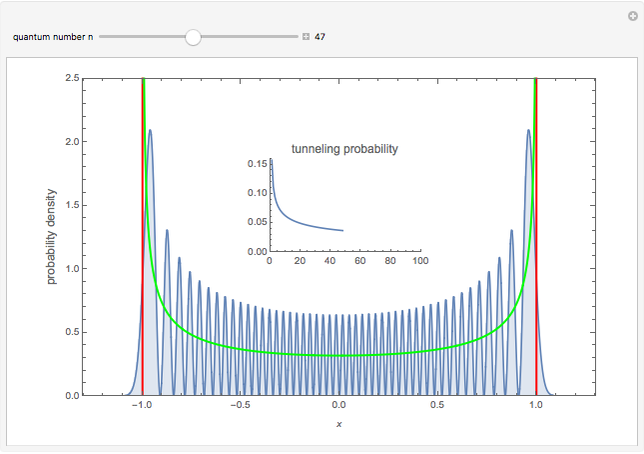
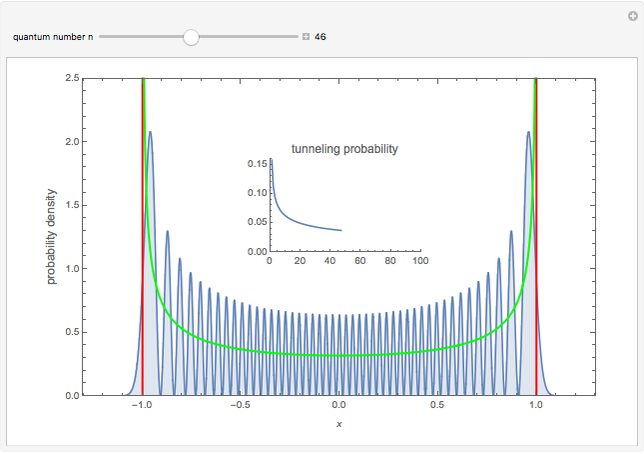
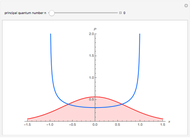
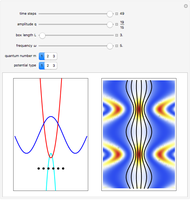
This Demonstration shows coordinate-space probability distributions for quantized energy states of the harmonic oscillator, scaled such that the classical turning points are always at  .
.
Contributed by: Arkadiusz Jadczyk (January 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Think about a classical oscillator, a swing, a weight on a spring, a pendulum in a clock…. They have a certain characteristic spring constant and a mass. For simplicity, choose units so that these constants are both 1. Also assume that the time scale is chosen so that the period is  . Given energy
. Given energy  , the classical oscillator vibrates with an amplitude
, the classical oscillator vibrates with an amplitude  . Its deviation
. Its deviation  from the equilibrium position
from the equilibrium position  is given by the formula
is given by the formula
 .
.
The relationship between energy  and amplitude
and amplitude  is simple:
is simple:  . For a classical oscillator, the energy
. For a classical oscillator, the energy  can be any positive number.
can be any positive number.
For a quantum oscillator, assuming units in which Planck's constant  , the possible values of energy are no longer a continuum but are quantized with the possible values:
, the possible values of energy are no longer a continuum but are quantized with the possible values:  . To each energy level there corresponds a quantum eigenstate; the wavefunction is given by
. To each energy level there corresponds a quantum eigenstate; the wavefunction is given by
 ,
,
where  is a Hermite polynomial. This wavefunction (notice that it is real valued) is normalized so that its square
is a Hermite polynomial. This wavefunction (notice that it is real valued) is normalized so that its square  gives the probability density of finding the oscillating point (with energy
gives the probability density of finding the oscillating point (with energy  ) at the point
) at the point  . Classically, there is zero probability for the particle to penetrate beyond the turning points
. Classically, there is zero probability for the particle to penetrate beyond the turning points  and
and  . But for the quantum oscillator, there is always a nonzero probability of finding the point in a classically forbidden region; in other words, there is a nonzero tunneling probability.
. But for the quantum oscillator, there is always a nonzero probability of finding the point in a classically forbidden region; in other words, there is a nonzero tunneling probability.
One popular quantum-mechanics textbook [3] reads: "The probability of being found in classically forbidden regions decreases quickly with increasing  , and vanishes entirely as
, and vanishes entirely as  approaches infinity, as we would expect from the correspondence principle."
approaches infinity, as we would expect from the correspondence principle."
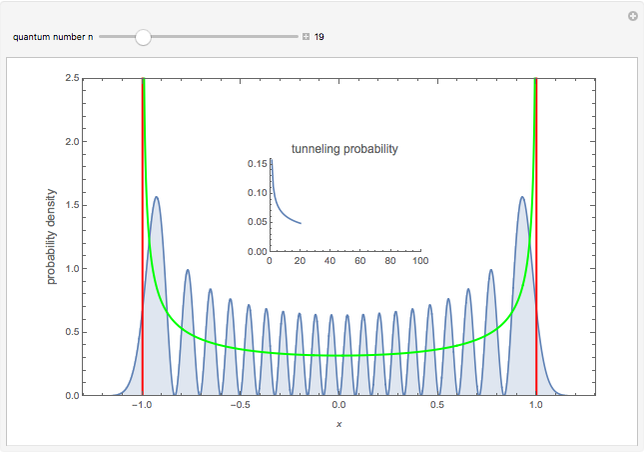
This Demonstration calculates these tunneling probabilities for  . The calculation is done symbolically to minimize numerical errors.
. The calculation is done symbolically to minimize numerical errors.
You can see the sequence of plots of probability densities, the classical limits, and the tunneling probability for each  . There is also a U-shaped curve representing the classical probability density of finding the swing at a given position given only its energy, independent of phase. Each graph is scaled so that the classical turning points are always at
. There is also a U-shaped curve representing the classical probability density of finding the swing at a given position given only its energy, independent of phase. Each graph is scaled so that the classical turning points are always at  and
and  . The vertical axis is also scaled so that the total probability (the area under the probability densities) equals 1.
. The vertical axis is also scaled so that the total probability (the area under the probability densities) equals 1.
It can be seen that indeed, the tunneling probability, at first, decreases rather rapidly, but then its rate of decrease slows down at higher quantum numbers  . While the tails beyond the red lines (at the classical turning points) are getting shorter, their height is increasing.
. While the tails beyond the red lines (at the classical turning points) are getting shorter, their height is increasing.
References
[1] J. L. Powell and B. Crasemann, Quantum Mechanics, Reading, MA: Addison-Wesley, 1961 p. 136.
[2] B. Thaller, Visual Quantum Mechanics: Selected Topics with Computer-Generated Animations of Quantum-Mechanical Phenomena, New York: Springer, 2000 p. 168.
[3] P. W. Atkins, J. de Paula, and R. S. Friedman, Quanta, Matter and Change: A Molecular Approach to Physical Chemistry, New York: Oxford University Press, 2009 p. 66.
Permanent Citation