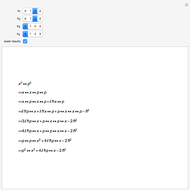
Harmonic Oscillator Eigenfunctions

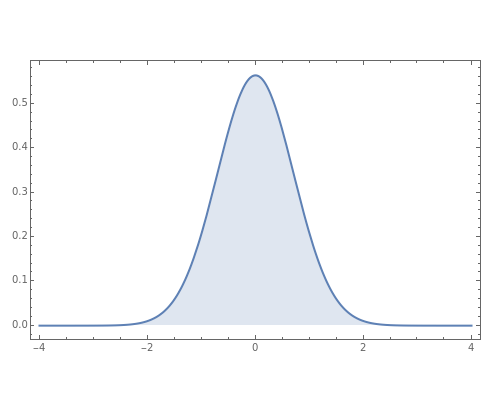
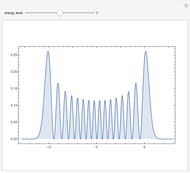
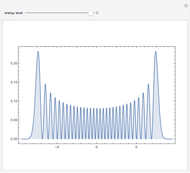
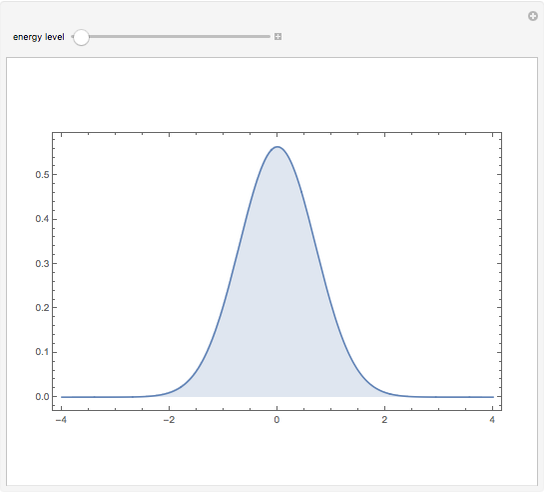
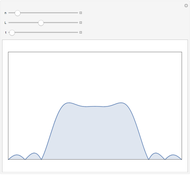
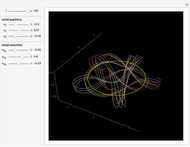
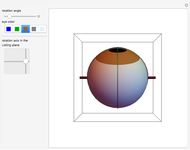
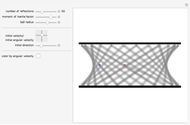
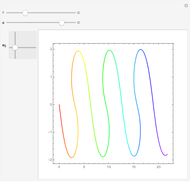
Absolute value of the harmonic oscillator eigenfunctions. The harmonic oscillator is the most important exactly solvable model of quantum mechanics. The ground state eigenfunction minimizes the uncertainty product. With increasing quantum number, the square of the absolute value of the eigenfunctions approaches the probability distribution of a classical particle in a harmonic potential with inverse square root singularities at the turning points.