Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Wigner Distribution Function for Harmonic Oscillator

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

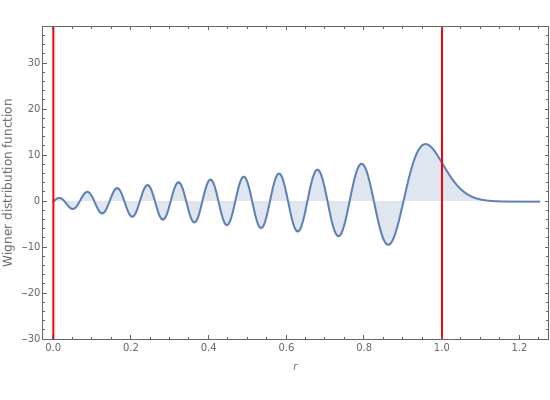
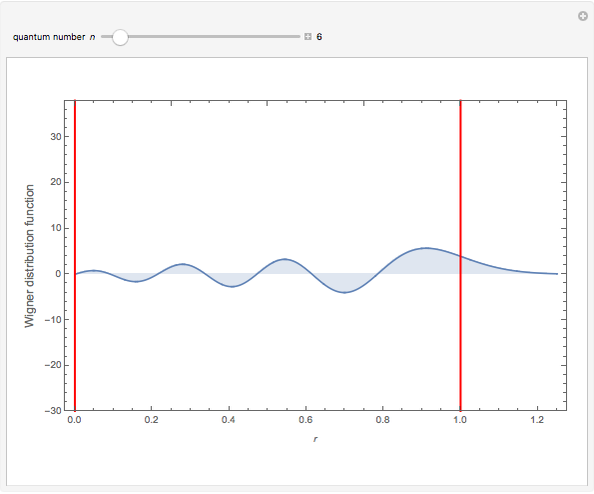
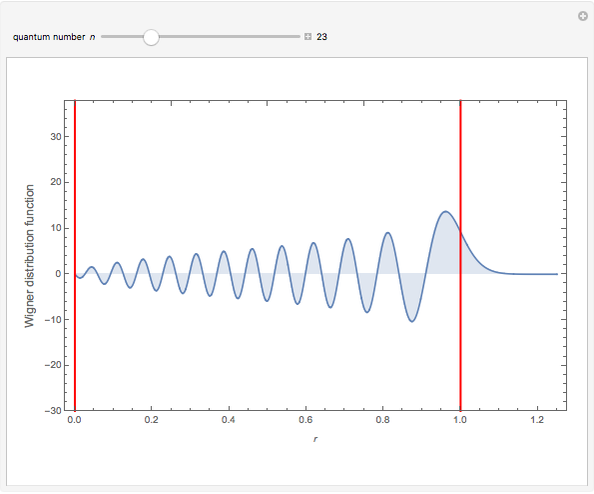
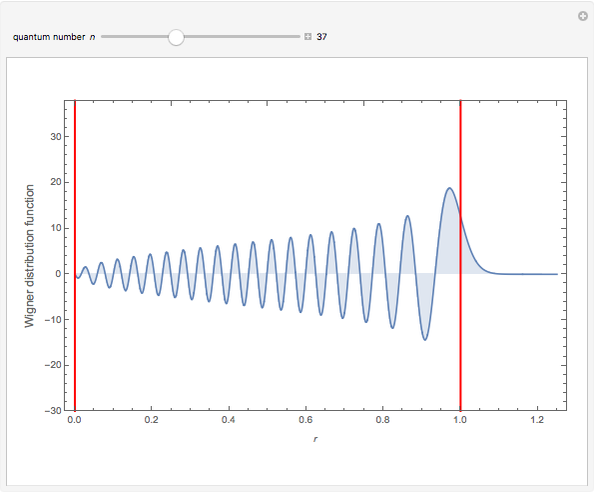
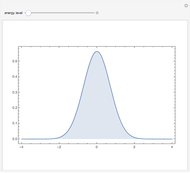
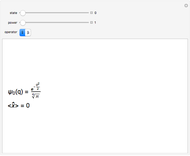
This Demonstration shows the Wigner quasiprobability distribution for 101 energy states of the quantum harmonic oscillator. Units are chosen so that the energy operator is simplified to

[more]

.

Quantized energy values are . Polar coordinates are used in the phase space. The Wigner radial quasiprobability distribution is defined by

,

noting that is real. The distribution is normalized and plotted as a function of . For each , the variable and the distribution are rescaled so that the classical turning points (normally at ) are all at .

[less]

Contributed by: Arkadiusz Jadczyk (January 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

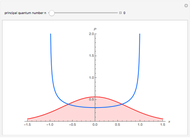
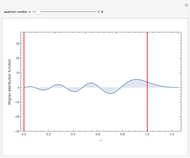
The vertical red line at indicates the classical turning point. Beyond this point is the classically forbidden region. The area under the plot to the right of this line is the quasiprobability of the nonclassical quantum tunneling behavior. For , this area is between 0.37 and 0.33. Yet, owing to the nonpositivity of the Wigner distribution, the meaning of these numbers is open to interpretation.

References

[1] Wikipedia. "Wigner Quasiprobability Distribution." (Jan 22, 2015) en.wikipedia.org/wiki/Wigner_quasiprobability_distribution.

[2] Wikipedia. "Quantum Harmonic Oscillator." (Jan 22, 2015) en.wikipedia.org/wiki/Quantum_harmonic_oscillator.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send