Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Ratios Involving Six Radii

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

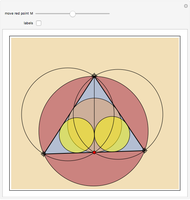
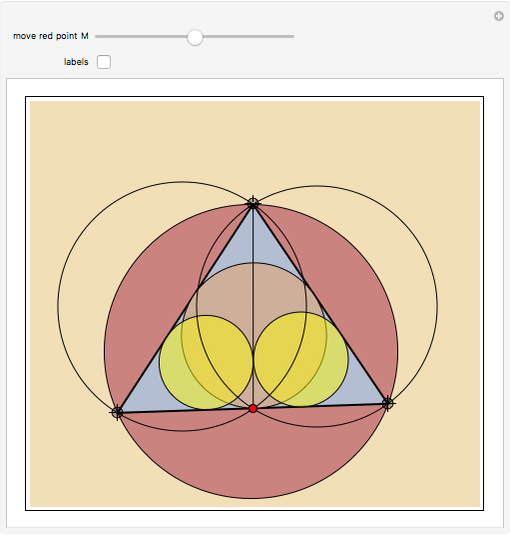
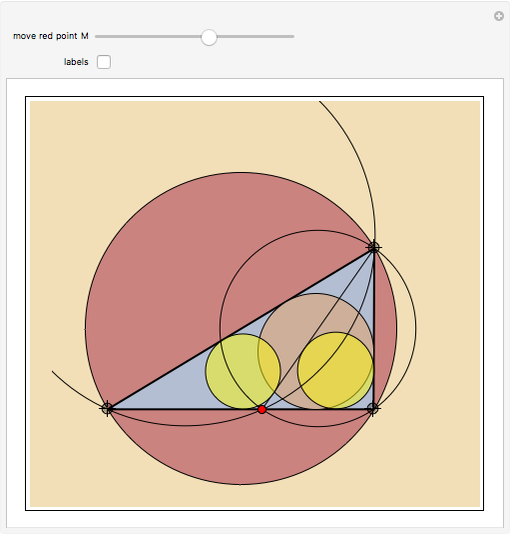
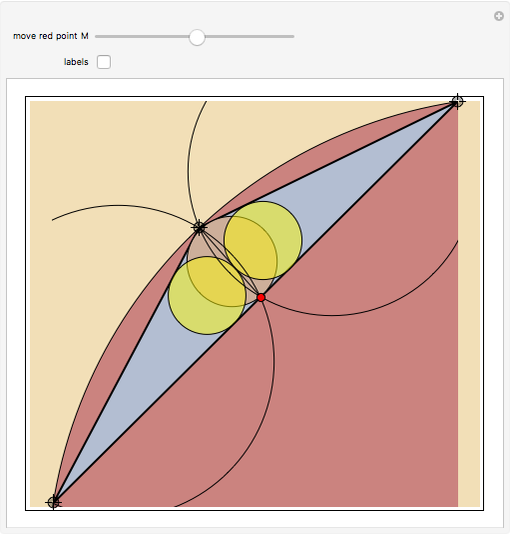
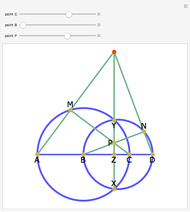
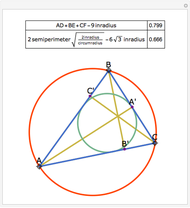
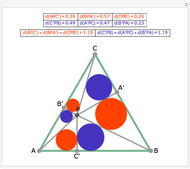
Given a point on the side of the triangle , let and be the radii of the inscribed circles of the triangles and , and let and be the radii of the circumcircles of the triangles and . Let and denote the radii of the inscribed circle and the circumcircle of the triangle , respectively. Prove that .

Contributed by: Jaime Rangel-Mondragon (July 2013)
Open content licensed under CC BY-NC-SA

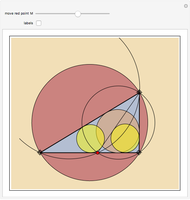
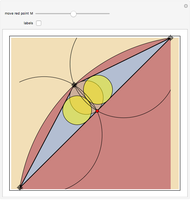
Snapshots

Details

The label for each radius is placed at the center of the circle of which it is the radius.

This Demonstration comes from problem 8 of the shortlisted problems for the 1970 International Mathematical Olympiad (IMO).

Reference

[1] D. Djukić, V. Janković, I. Matić, and N. Petrović, The IMO Compendium, 2nd ed., New York: Springer, 2011 p. 69.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send