Records in Sequences of Random Variables

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Consider a sequence of real numbers 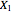 ,
, 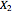 , …. A value
, …. A value 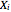 is a record value (or a high-water mark) if it is the largest value among all the values that have been recorded up to time
is a record value (or a high-water mark) if it is the largest value among all the values that have been recorded up to time  ;
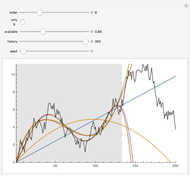
; 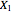 is always a record. This Demonstration shows a sample for one of three distributions and its records with a red color. The Demonstration also shows the distribution of the number of records for samples of sizes 10, 20, …, 1000; the distribution of the occurrence time of the
is always a record. This Demonstration shows a sample for one of three distributions and its records with a red color. The Demonstration also shows the distribution of the number of records for samples of sizes 10, 20, …, 1000; the distribution of the occurrence time of the 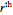 record,
record, 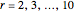 ; and the conditional upper bounds of waiting times for the next record.
; and the conditional upper bounds of waiting times for the next record.
Contributed by: Heikki Ruskeepää (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
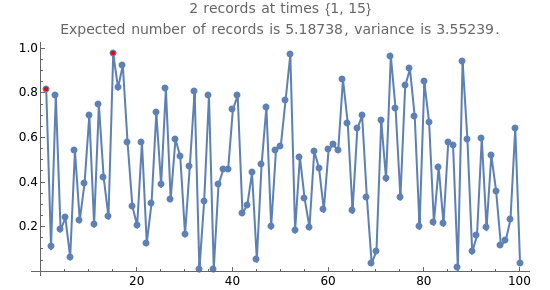
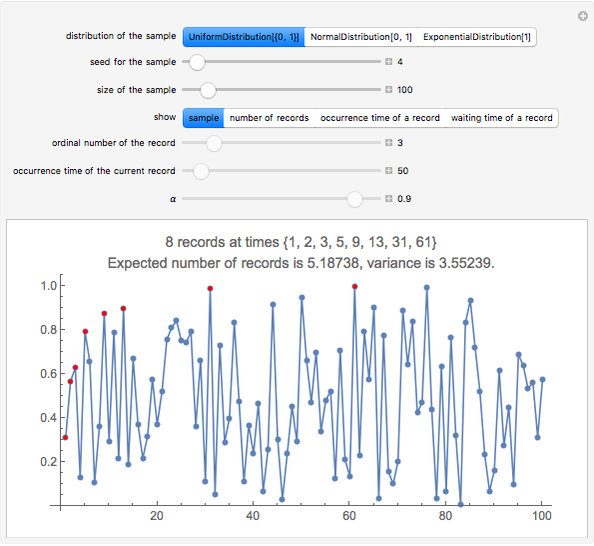
Snapshot 1: Among the 100 observations from a uniform distribution, there happen to be 8 records; the expected number of records for a series of 100 values is 5.2.
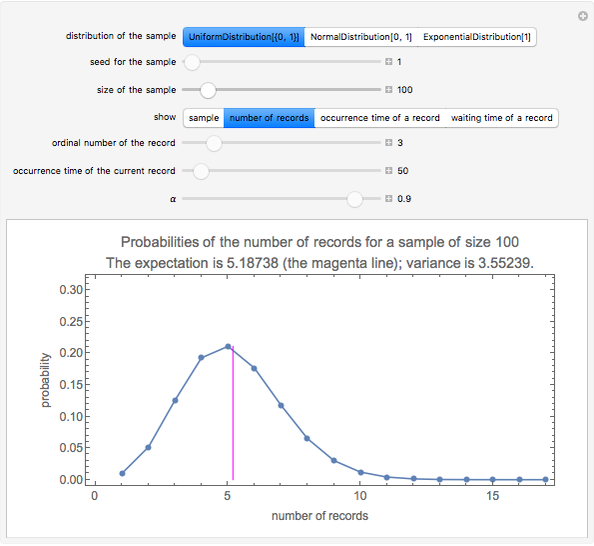
Snapshot 2: Here are the probabilities that there are 1, 2, …, 17 records in a series of 100 values. The magenta line is at the expectation 5.2. There is a very small probability that there are more than, say, 10 records among 100 values. Theoretically, there could be as few as one record (it has approximately a probability of 0.01) and as many as 100 records (which must have a very tiny probability). The Demonstration only shows the probabilities up to the 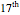 record.
record.
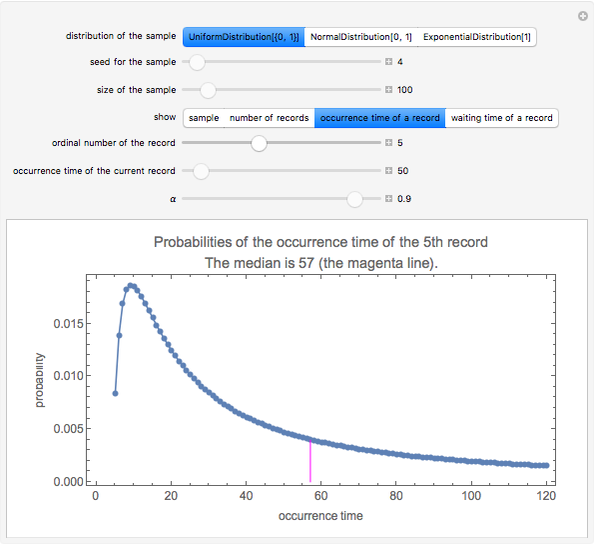
Snapshot 3: This plot shows the probabilities of the occurrence times of the fifth record. The earliest occurrence time is 5 (it has a probability of approximately 0.008). The most probable occurrence time is 9 (with a probability of approximately 0.019). The median is 57 (the mean is infinite). Thus, with several sequences, in approximately half of them the fifth record is among the first 57 values; in another half of the sequences, the fifth record occurs later. There is no upper bound for the occurrence time of the fifth record; it could be, say, larger than 1000. The Demonstration only shows the probabilities of some small values of the occurrence time.
Snapshot 4: The plot shows conditional upper bounds for the waiting times of records. In the first snapshot, the seventh record occurred at time 31. Given that the occurrence time of a record is 31, the plot shows that the next record is among the next 279 values with probability 0.9; with probability 0.1, more values are needed to get the next record (from the first snapshot, the next record (the eighth) was actually the 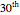 value after the seventh record).
value after the seventh record).
Expected Number of Records
Let 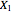 , …,
, …,  be independent, identically distributed continuous random variables. Let
be independent, identically distributed continuous random variables. Let 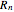 be the total number of records in the sequence
be the total number of records in the sequence 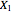 , …,
, …,  . The expected value of
. The expected value of 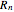 is
is  , that is,
, that is, 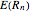 is the
is the 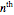 harmonic number. For example, for sequences of length 10, 100, 1000, 10000, 100000, or 1000000 the expected number of records is 2.9, 5.2, 7.5, 9.8, 12.1, and 14.4, respectively. The lengths of the sequence needed so that the expected number of records for the first time is at least 2, 3, …, 10 are 4, 11, 31, 83, 227, 616, 1674, 4550, and 12367, respectively. For example, for the mean number of records to be 10, we need a sequence of 12,367 values, which is the number of terms in the harmonic series required to make the sum exceed 10. Near the beginning of the sequence, records occur quite frequently, but after that, new records occur increasingly seldom. Thus, except initially, records are seldom.
harmonic number. For example, for sequences of length 10, 100, 1000, 10000, 100000, or 1000000 the expected number of records is 2.9, 5.2, 7.5, 9.8, 12.1, and 14.4, respectively. The lengths of the sequence needed so that the expected number of records for the first time is at least 2, 3, …, 10 are 4, 11, 31, 83, 227, 616, 1674, 4550, and 12367, respectively. For example, for the mean number of records to be 10, we need a sequence of 12,367 values, which is the number of terms in the harmonic series required to make the sum exceed 10. Near the beginning of the sequence, records occur quite frequently, but after that, new records occur increasingly seldom. Thus, except initially, records are seldom.
As a practical example [1, p. 65], assume that the maximum yearly temperatures in a given city can be considered to be values of approximately independent, identically distributed random variables. A person at the ages 4, 11, 31, or 83 years has seen 2, 3, 4, and 5 temperature records on average, respectively.
As another example [1, p. 78], to find the weakest board among 100 boards, stress the first board to its failure point. Stop the test of the second board if it survives the stress applied to the first board. By continuing similarly with the rest of the boards, the expected number of broken boards is only 5.2.
Distribution of the Number of Records
Let  be the probability that in a series of length
be the probability that in a series of length  there will be exactly
there will be exactly  records. Rényi showed that
records. Rényi showed that  where
where 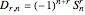 and
and 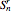 is a Stirling number of the first kind. For example, in a sequence of length 6, the probabilities that there will be 1, 2, 3, 4, 5, or 6 records are 0.1667, 0.3806, 0.3125, 0.1181, 0.0208, and 0.0014, respectively.
is a Stirling number of the first kind. For example, in a sequence of length 6, the probabilities that there will be 1, 2, 3, 4, 5, or 6 records are 0.1667, 0.3806, 0.3125, 0.1181, 0.0208, and 0.0014, respectively.
Occurrence Time of a Record
Let 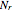 be the time at which we have the
be the time at which we have the  record (
record ( ). It can be shown that
). It can be shown that 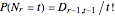 ,
, 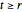 , where
, where 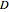 is as before. The expected value of
is as before. The expected value of 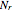 is infinite for
is infinite for 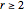 . This Demonstration shows the median of the distribution of
. This Demonstration shows the median of the distribution of 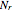 . The medians for
. The medians for  = 2, 3, …, 10, are 2, 7, 21, 57, 157, 430, 1173, 3199, and 8717, respectively. For example, consider a large number of independent sequences; in about half of them the fifth record occurs no later than at time 57 and in the other half of them the fifth record occurs later than at time 57.
= 2, 3, …, 10, are 2, 7, 21, 57, 157, 430, 1173, 3199, and 8717, respectively. For example, consider a large number of independent sequences; in about half of them the fifth record occurs no later than at time 57 and in the other half of them the fifth record occurs later than at time 57.
Waiting Time to the Next Record
Let 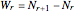 be the interrecord waiting time, that is, the time elapsed between the
be the interrecord waiting time, that is, the time elapsed between the 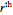 and the
and the 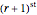 records. The conditional distribution of
records. The conditional distribution of 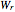 , conditioned on
, conditioned on 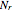 , is
, is  . An
. An 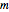 such that this probability is a given value
such that this probability is a given value  is
is 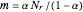 . For example, if
. For example, if  is 0.5, 0.9, 0.95, or 0.99, then
is 0.5, 0.9, 0.95, or 0.99, then 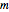 is
is 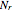 ,
,  ,
, 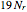 , and
, and 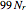 , respectively. This means that
, respectively. This means that
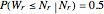 ,
,
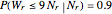 ,
,
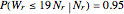 ,
,
 .
.
For example, if the current record (the 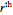 record) occurred at time
record) occurred at time 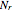 , then with probability 0.5 the next record is among the next
, then with probability 0.5 the next record is among the next 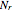 values; with probability 0.5, more values are needed to get the next record. Similarly, with probability 0.9, the next record is among the next
values; with probability 0.5, more values are needed to get the next record. Similarly, with probability 0.9, the next record is among the next  values.
values.
As a numerical example, let the fifth record occur at time 50: 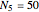 . Then
. Then 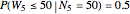 , that is, the sixth record with probability 0.5 is among the next 50 values; with probability 0.5, we have to wait longer. As another example,
, that is, the sixth record with probability 0.5 is among the next 50 values; with probability 0.5, we have to wait longer. As another example,  is 450 so that
is 450 so that 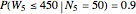 , that is, the sixth record with probability 0.9 is among the next 450 values.
, that is, the sixth record with probability 0.9 is among the next 450 values.
A Note
Not one of the results mentioned here depends on the actual distribution of the variables 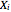 ; we only need the assumption that these variables are independent, identically distributed, continuous random variables. In this Demonstration, the choices between uniform, normal, and exponential variables are offered only to show that, for each distribution, the samples have similar properties for records.
; we only need the assumption that these variables are independent, identically distributed, continuous random variables. In this Demonstration, the choices between uniform, normal, and exponential variables are offered only to show that, for each distribution, the samples have similar properties for records.
The Demonstration is based on [1, pp. 63–78].
Reference
[1] J. Andel, Mathematics of Chance, New York: Wiley, 2001.
Permanent Citation