Method of Support Vector Regression

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
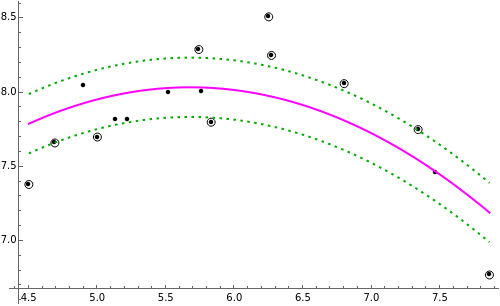
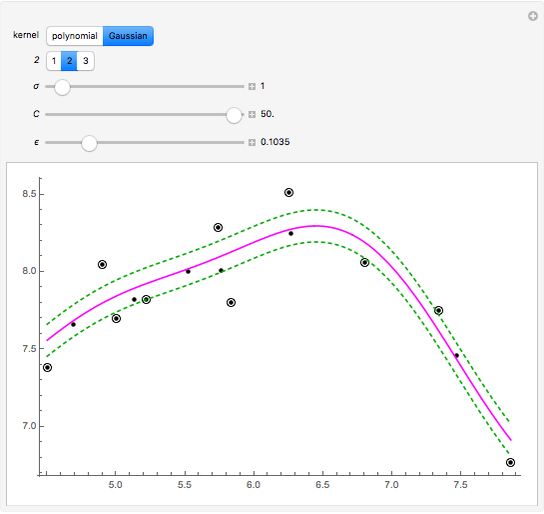
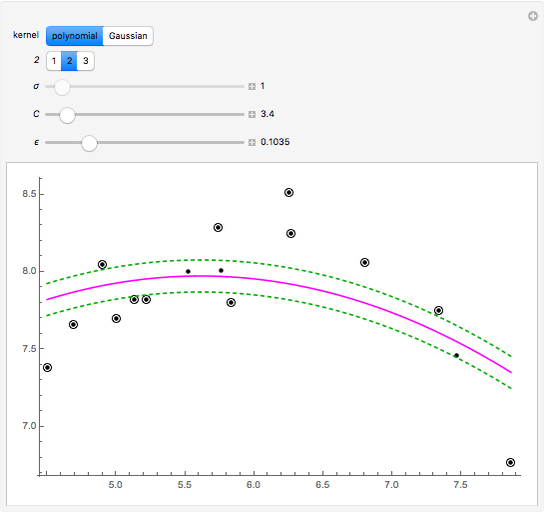
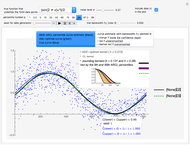
This Demonstration uses the method of support vector regression to calculate curves representing chemical data. The regression curve is shown in magenta. The margins (dashed green curves) are at distance  from the regression curve. The circled black points outside of the margins are the support vectors; the points inside the margins could be deleted and the regression curve would not change. The method of support vector regression uses kernels: here either a polynomial kernel (of degree 1, 2 or 3) or a Gaussian kernel (with parameter
from the regression curve. The circled black points outside of the margins are the support vectors; the points inside the margins could be deleted and the regression curve would not change. The method of support vector regression uses kernels: here either a polynomial kernel (of degree 1, 2 or 3) or a Gaussian kernel (with parameter  ). You can vary the parameter
). You can vary the parameter  to adjust the weights given to the fitting errors from the curve to the support vectors.
to adjust the weights given to the fitting errors from the curve to the support vectors.
Contributed by: Heikki Ruskeepää (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
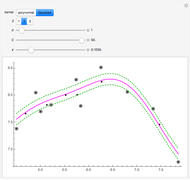
Snapshot 1: for small  , most points are support vectors
, most points are support vectors
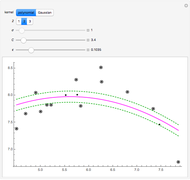
Snapshot 2: for small  , very little weight is given to discrepancies between the fit and the support vectors, so that the fit follows the data only approximately
, very little weight is given to discrepancies between the fit and the support vectors, so that the fit follows the data only approximately
Snapshot 3: with a Gaussian kernel, a small  causes the fit to follow the data very closely
causes the fit to follow the data very closely
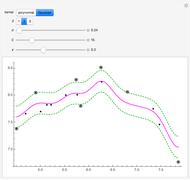
Snapshot 4: with a larger  , the fit follows the data less accurately
, the fit follows the data less accurately
The data used in this Demonstration is from [1].
For a detailed derivation and explanation of the method of support vector regression, see the document cited in Related Links. In that document, we arranged a small competition in which we studied the performance of support vector regression and seven other prediction methods when applied to 11 datasets. Support vector regression was the winner of that competition.
Reference
[1] O. Ivanciuc, "Applications of Support Vector Machines in Chemistry," in Reviews in Computational Chemistry, Vol. 23 (K. B. Lipkowitz and T. R. Cundari, eds.), Weinheim: Wiley-VCH, 2007 pp. 291–400.
Permanent Citation