Recursive Exercises II: A paradox

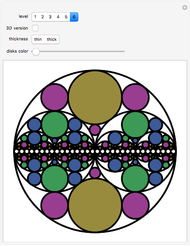
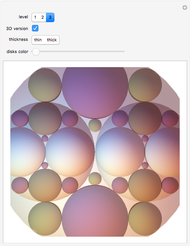
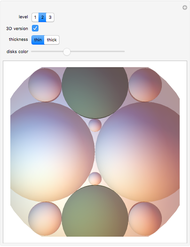
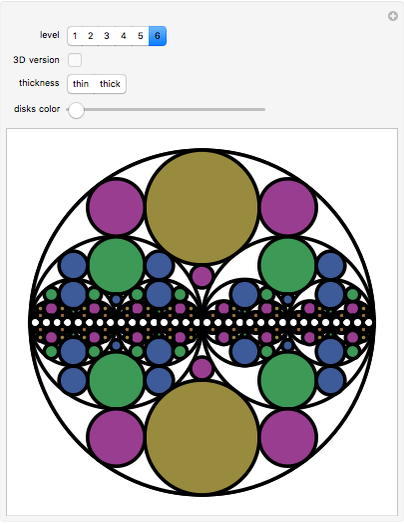
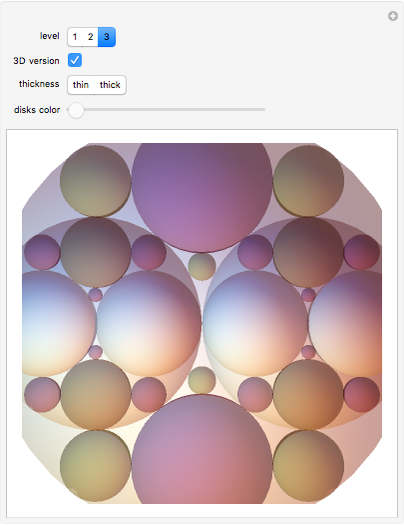
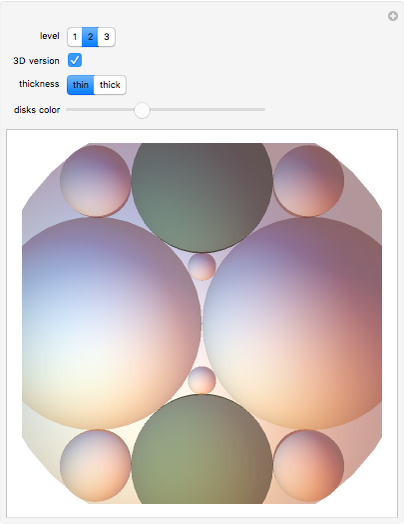
This Demonstration produces a series of shapes based on the recursive nesting of circles. As the process is repeated, consider what happens to the circles with white interiors whose centers lie on the largest horizontal diameter. Gather all those circles into families sharing the same radius. There are 1, 2, 4, 8, … circles in each of those families. The sum of the circumferences of the circles in each family is always the same number . Suppose the largest circle has diameter 1, that is . Then, as you increase the level, the white circles converge to the largest horizontal diameter and the conclusion is that !