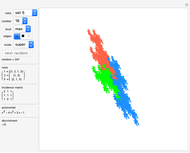
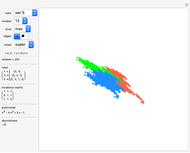
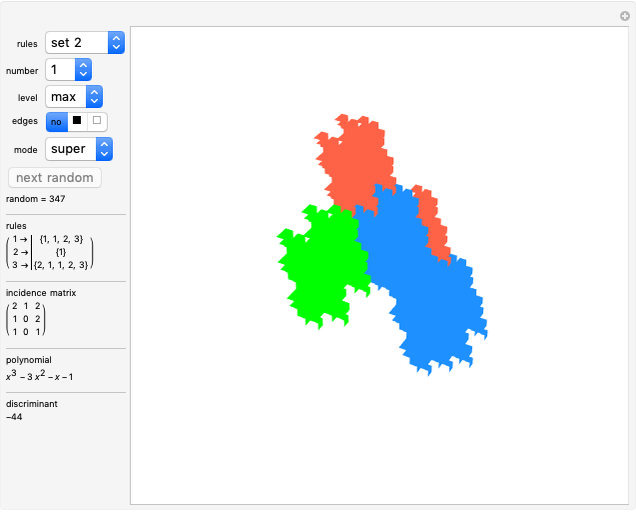
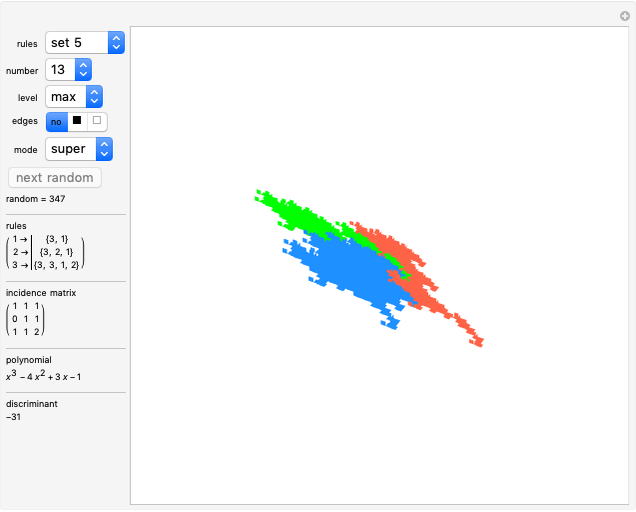
Rauzy Fractals as Stepped Surfaces

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
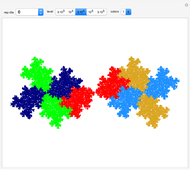
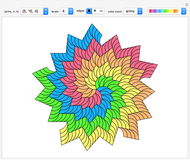
Experiment with Rauzy fractals and select related tilings from hundreds of given examples.
Contributed by: Dieter Steemann (April 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
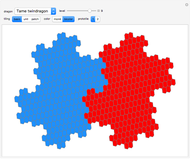
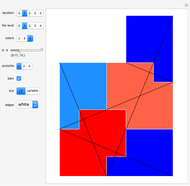
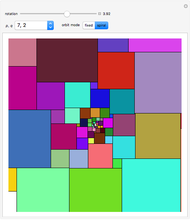
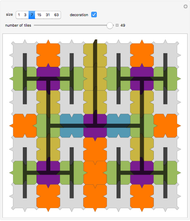
An introduction to Pisot substitutions and Rauzy fractals is given by Arnoux and Ito [1]. A Rauzy fractal is a fractal set associated with the Tribonacci substitution. All provided substitutions are unimodular and of the Pisot type. Pisot means that the substitution has an incidence matrix with a unique eigenvalue of modulus greater than 1, and all other eigenvalues of modulus less than 1. Unimodular refers to a matrix with a determinant of  . Such tilings (regarding the arrangement of prototiles for an iteration level tending to infinity) may have a discrete spectrum and are translation aperiodic, that is, are quasi-periodic. The super tiles, meaning the union of prototiles at a specific iteration level, still tile periodically.
. Such tilings (regarding the arrangement of prototiles for an iteration level tending to infinity) may have a discrete spectrum and are translation aperiodic, that is, are quasi-periodic. The super tiles, meaning the union of prototiles at a specific iteration level, still tile periodically.
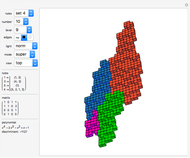
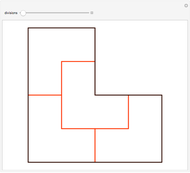
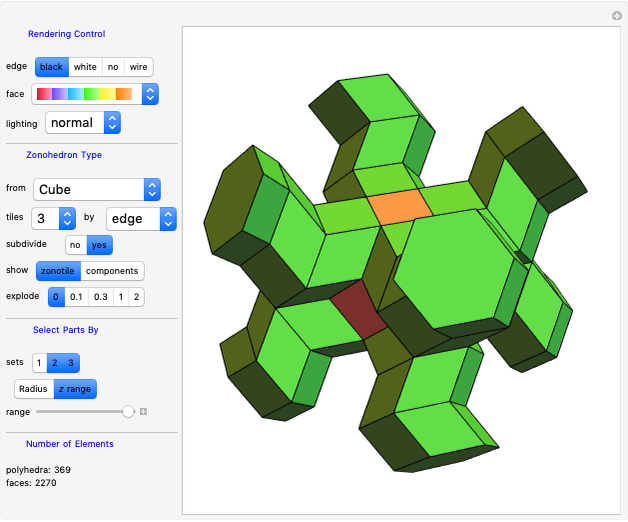
The core algorithms of this program follow the work of Barge and Kwapisz [2]. The tilings are defined by substitution rules using an alphabet of three letters ( in this case). The generated output is a so-called stepped surface, where each letter of the substitution result corresponds to a specific 3D face (prototile). These faces are projected into the 2D view plane using the corresponding eigenvector of the Pisot eigenvalue. This can be experienced by manual rotation of the image result, best at low iteration levels and with colored edges. All rules in the six fixed rule sets are different, but results may include symmetries. Most rules originate from our own experiments. The random rule set is selected from an arbitrary subset using at most three letters per substitution. Over 700 examples are provided, but many more are possible. The first member in rule set 1 is the famous Tribonacci (Rauzy) substitution.
in this case). The generated output is a so-called stepped surface, where each letter of the substitution result corresponds to a specific 3D face (prototile). These faces are projected into the 2D view plane using the corresponding eigenvector of the Pisot eigenvalue. This can be experienced by manual rotation of the image result, best at low iteration levels and with colored edges. All rules in the six fixed rule sets are different, but results may include symmetries. Most rules originate from our own experiments. The random rule set is selected from an arbitrary subset using at most three letters per substitution. Over 700 examples are provided, but many more are possible. The first member in rule set 1 is the famous Tribonacci (Rauzy) substitution.
Controls
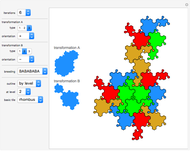
rules: Use this popup menu to select one of the six fixed rule sets; “random” activates the random selection from a collection of more than 600 rules.
number: Use this popup menu to select a specific member of the current rule set; this is deactivated when random is active.
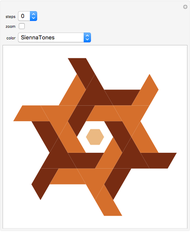
level: Use this popup menu to set the iteration level. The level is limited so that the estimated number of tiles is less than 15,000. Level 0 shows the three prototiles. Level 1 shows the initial arrangement of prototiles. "max" sets a level according to the limit count of tiles.
edges: Use this setter bar to select how the tile edges are depicted.
mode: "super" tiles inherit color from their predecessor, so super tiles become visible. "proto" means colored according to the prototiles.
next random: Click this button in order to get the next random rule; this is deactivated when a fixed rule set is active.
References
[1] P. Arnoux and S. Ito, "Pisot Substitutions and Rauzy Fractals," Bulletin of the Belgian Mathematical Society, 8, 2001 pp. 181–207. (Mar 21, 2018) iml.univ-mrs.fr/~arnoux/ArnouxIto.pdf.
[2] M. Barge and J. Kwapisz, "Geometric Theory of Unimodular Pisot Substitutions," American Journal of Mathematics, 128(5), 2006 pp. 1219–1282. www.jstor.org/stable/40068030.
Permanent Citation