Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Regular n-Gons as Polygons and Stars

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

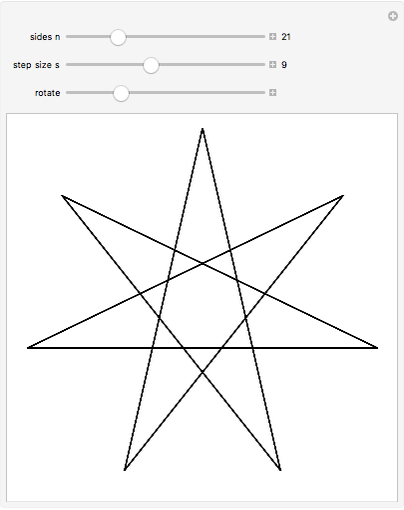
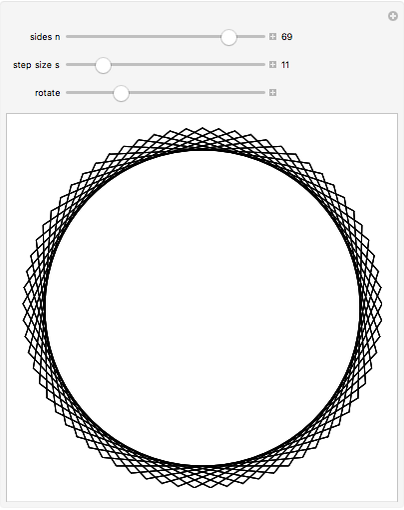
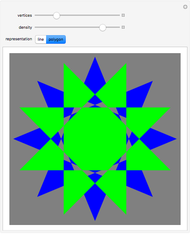
This Demonstration shows regular -gons that can be convex polygons or stars.

[more]

Polygons with sides correspond to step size 1: the sides are connected in sequence around the inscribed circle, which they approximate as the number of sides increases.

With sides and a larger step size , the figure is a star or a polygon with sides if this is a whole number.

[less]

Contributed by: Arthur Stammet (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

It's an interesting job to look for all the pentagons and pentagrams and to take note of the relationships between the number of sides and the divisor (step size).

The series of pentagons is , , , , …, , which are all equal to 5. Beginning with , double the values of the divisor in order to get pentagrams.

The series of pentagrams is therefore , , , , , …, .

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send