Relations and Functions between Small Sets

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
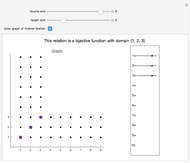
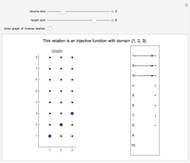
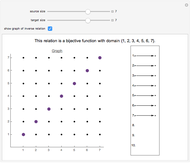
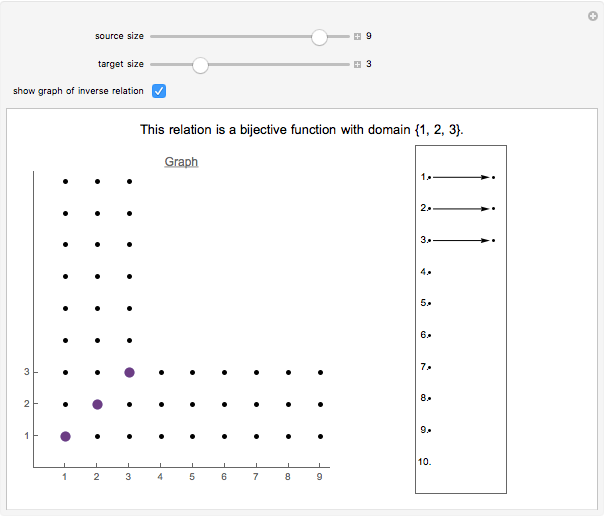
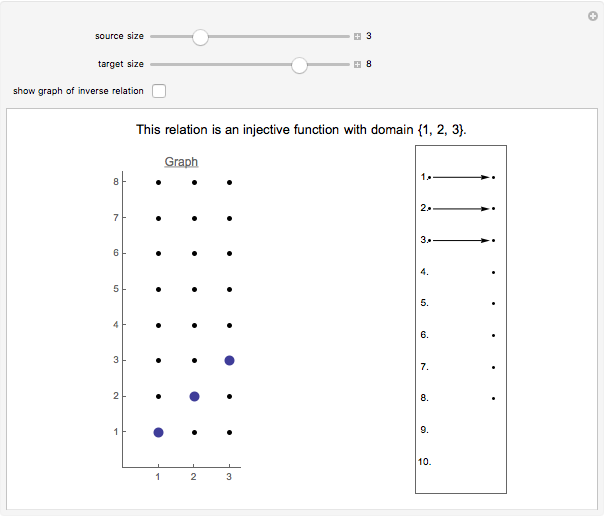
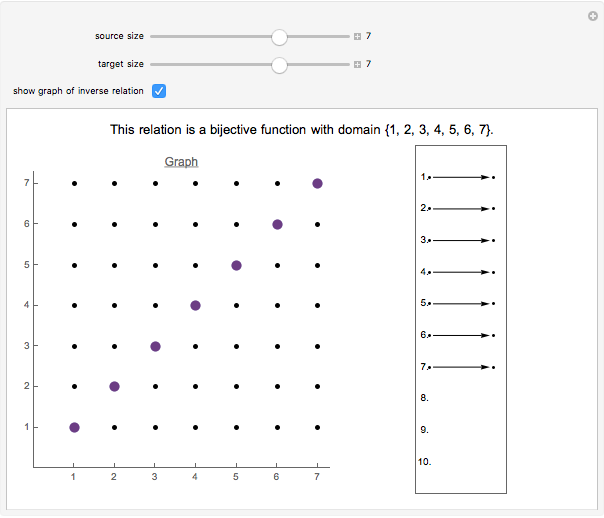
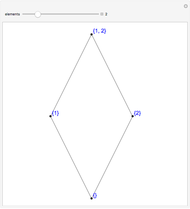
A relation between two sets is a subset of their Cartesian product. The subset's pairs are plotted in the graph. Click the dots on the left to add or delete pairs from the relation.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A relation between two sets 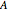 and
and 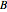 is a subset of the Cartesian product
is a subset of the Cartesian product 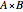 ;
; 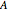 is called the source set and
is called the source set and 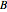 is called the target set. If
is called the target set. If 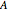 contains
contains  elements and
elements and 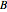 contains
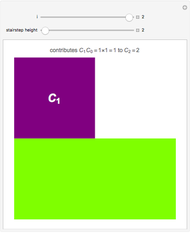
contains  elements, there are
elements, there are 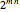 relations between
relations between 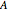 and
and 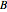 . If
. If 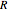 is a relation between
is a relation between 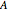 and
and 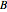 , the inverse of
, the inverse of 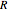 is the subset of
is the subset of  consisting of all pairs
consisting of all pairs 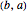 where
where 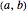 belongs to
belongs to 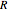 .
.
A function is a relation that contains no two pairs with the same first coordinate and distinct second coordinates. A function can be thought of as a rule that assigns to each element in a subset of the source (called the domain now) exactly one element in the target. The range is the subset of the target that consists of elements to which some element of the domain has been assigned. The function maps the domain to the range, and if a function called 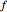 assigns an element
assigns an element  to an element
to an element 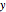 , it is written as
, it is written as  . The relation that defines a function, that is, the collection of all pairs of the form
. The relation that defines a function, that is, the collection of all pairs of the form 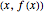 for
for  in the domain, is called the graph of the function.
in the domain, is called the graph of the function.
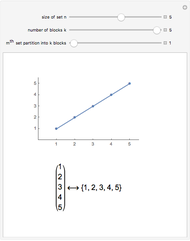
There are 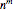 different functions that map an
different functions that map an  -element domain into an
-element domain into an  -element target. (The sets in question must be finite for any formulas to do with
-element target. (The sets in question must be finite for any formulas to do with  and
and  , but the definitions apply to infinite sets such as the real numbers.)
, but the definitions apply to infinite sets such as the real numbers.)
A function is one-to-one (also called an injection) if no two elements of the domain are assigned to the same element of the range. Visually, a function is one-to-one if no horizontal line intersects its graph more than once. The inverse of a function is itself a function if and only if the function is an injection. For any injections to exist, the target must be at least as large as the domain, that is, 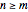 , in which case there are
, in which case there are 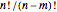 injections mapping an
injections mapping an  -element domain into an
-element domain into an  -element target.
-element target.
A function is onto (also called a surjection) if the target and the range are the same set. For any surjections to exist, the domain must be at least as large as the target, that is,  , in which case there are
, in which case there are 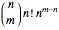 surjections mapping an
surjections mapping an  -element domain onto an
-element domain onto an  -element range.
-element range.
A function that is both one-to-one and onto is called a bijection. For any bijections to exist, the domain and target must be the same size, that is, 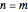 , in which case there are
, in which case there are  bijections mapping one
bijections mapping one  -element set to another.
-element set to another.
Permanent Citation