Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

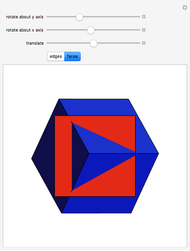
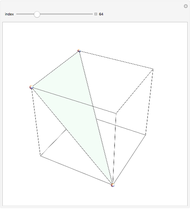
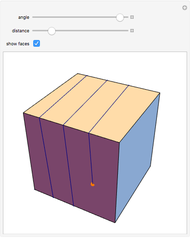
Small Set Partitions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

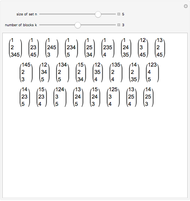
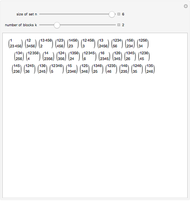
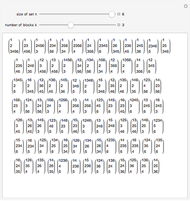
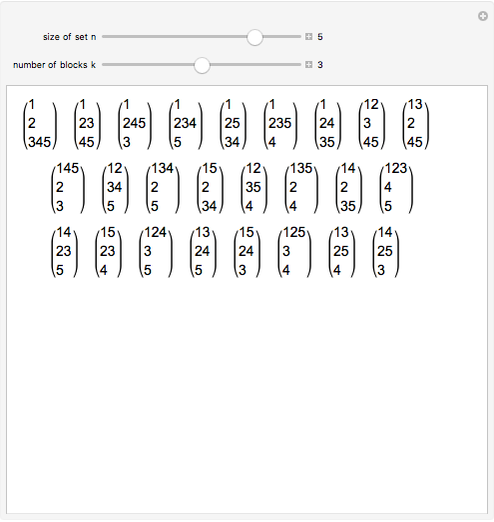
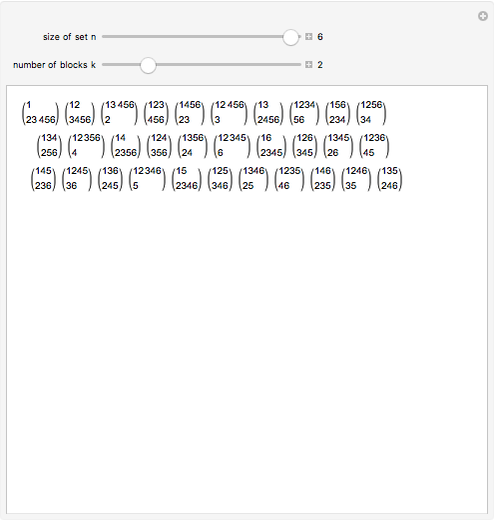
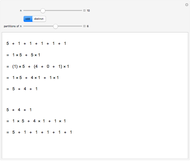
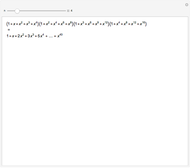
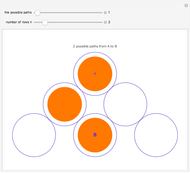
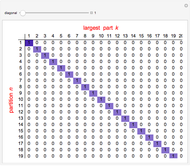
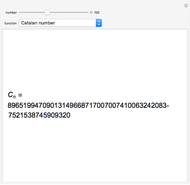
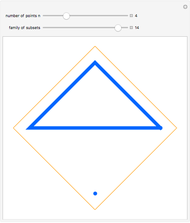
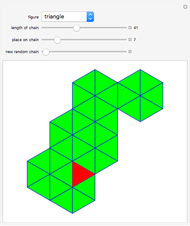
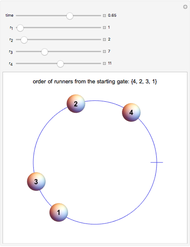
This Demonstration shows the partitions of the set into blocks, where and are small. For example, you could split into the blocks , , and . This is written compactly as .

[more]

The number of ways of partitioning a set of elements into nonempty subsets (or blocks) is the Stirling number of the second kind, . The total number of ways to partition a set into blocks is the Bell number .

[less]

Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send