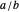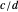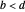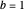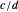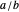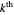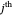Repeated Mediants Lead to Iterative Brackets

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
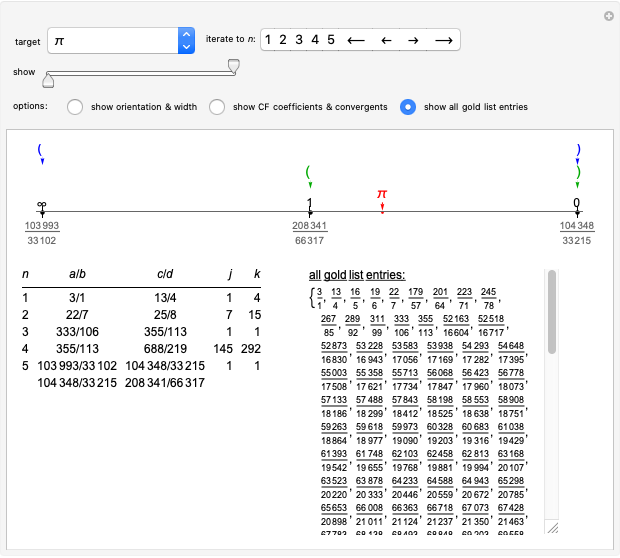
This Demonstration shows initial steps in the iterative bracket method for creating the gold list of increasingly close rational approximants of a given real number target. (See the Details for definitions and examples.)
[more]
Contributed by: R. Lewis Caviness and Kenneth E. Caviness (December 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The iterative bracket method used here is based on several related concepts; you can experiment with all of them.
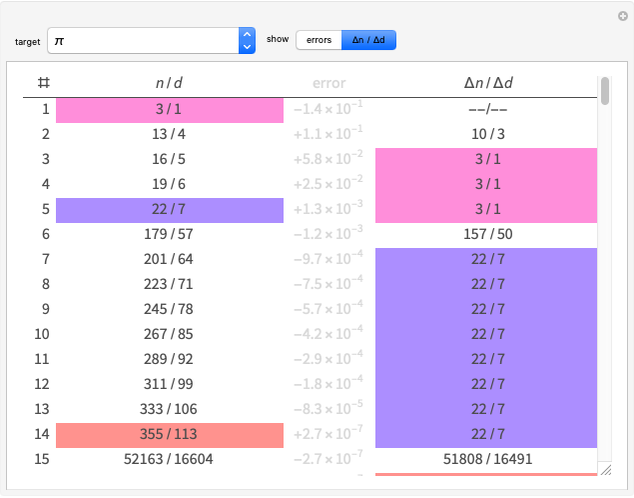
An approximant of a real number target  is a rational approximation to
is a rational approximation to  , with the best choice of numerator for the given denominator. For example, if
, with the best choice of numerator for the given denominator. For example, if 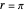 , then 22 is the best numerator for the denominator 7.
, then 22 is the best numerator for the denominator 7.
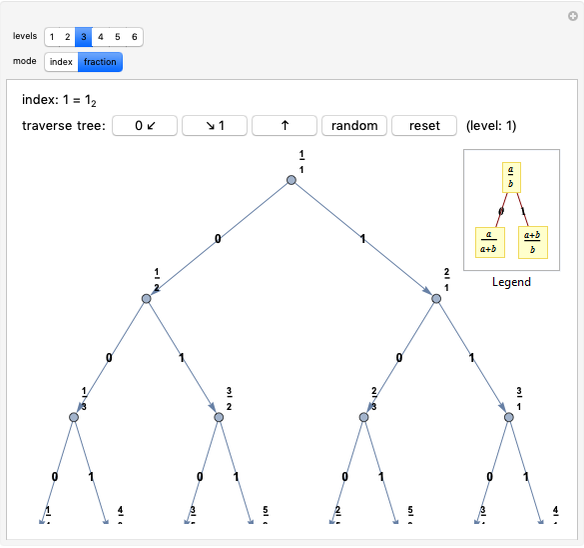
The list of approximants of 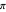 , with every integral denominator, starts as:
, with every integral denominator, starts as:
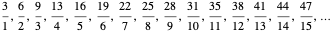 .
.
This list reduces to the gold list by excluding all entries that are not closer to the target than previous entries: 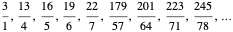 . For example,
. For example, 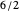 and
and 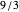 are dropped from the list because they are not closer to
are dropped from the list because they are not closer to 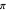 than
than 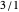 ; similarly these are dropped
; similarly these are dropped 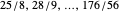 because they are not closer to
because they are not closer to 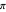 than
than 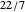 , and so on.
, and so on.
The original motivation for the iterative bracket algorithm was this serendipitous observation: generally, the fractions 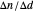 formed from differences in numerators and denominators of successive gold list entries are themselves previous gold list entries! In the case of
formed from differences in numerators and denominators of successive gold list entries are themselves previous gold list entries! In the case of 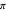 , these fractional differences are
, these fractional differences are 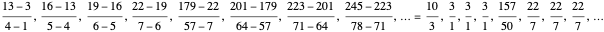 . Beyond the runs of
. Beyond the runs of 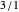 and
and 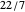 , we also noticed a run of
, we also noticed a run of 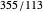 , an even better approximation to
, an even better approximation to 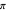 .
.
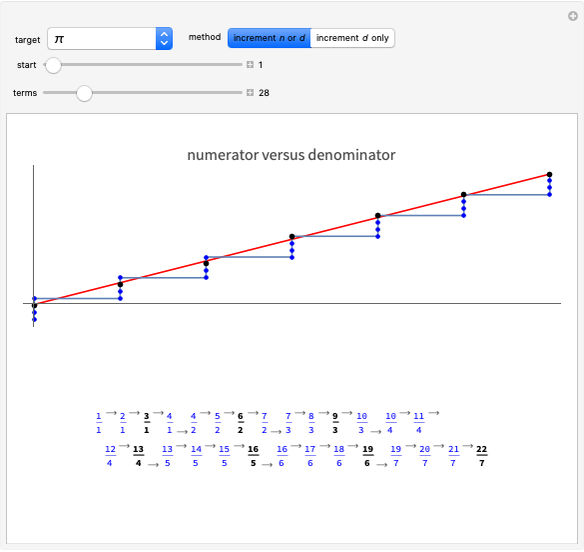
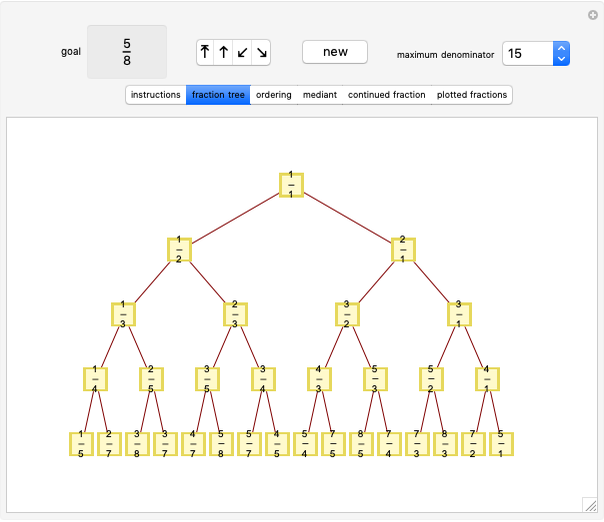
Of course, fractions are not added or subtracted this way, as generations of basic math teachers have explained to their students. But surprisingly, in most cases each new gold list element is the mediant, also known as the Farey mean or "freshman sum", of earlier entries. Many consecutive subsequences of the gold list consist of weighted mediants of fractions with smaller denominators.
Definition: The mediant of fractions 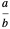 and
and 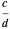 is
is 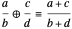 .
.
Definition: The weighted mediant of fractions 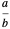 and
and 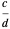 with weighting factor
with weighting factor  is
is 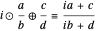 , where the nonnegative integer
, where the nonnegative integer  weights the earlier fraction
weights the earlier fraction 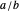 , the one with the smaller denominator.
, the one with the smaller denominator.
Example: For 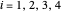 , the subsequence
, the subsequence 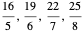 is formed by four weighted mediants of
is formed by four weighted mediants of  and
and 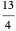 :
:  .
.
Definition: The nonnegative fraction pair 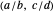 forms a bracket for the positive real-number target
forms a bracket for the positive real-number target  if and only if
if and only if 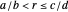 or
or 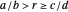 . By convention, the earlier fraction, the one with the smaller denominator, is written first, that is,
. By convention, the earlier fraction, the one with the smaller denominator, is written first, that is, 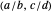 , where
, where 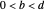 . Each bracket
. Each bracket 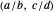 is associated with an interval, either
is associated with an interval, either 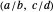 or
or 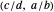 , where here the usual convention lists the interval endpoints in ascending order. The real number
, where here the usual convention lists the interval endpoints in ascending order. The real number  is considered to lie inside the bracket
is considered to lie inside the bracket 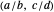 if it is in the corresponding interval. The length of bracket
if it is in the corresponding interval. The length of bracket 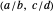 is given by
is given by 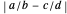 . For irrational targets, all intervals are open. For a rational target, however, it is possible for the target to equal the later fraction. (All the targets listed are irrational with the possible exception of Euler
. For irrational targets, all intervals are open. For a rational target, however, it is possible for the target to equal the later fraction. (All the targets listed are irrational with the possible exception of Euler 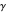 .)
.)
Example: The first bracket for 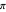 is
is 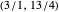 ; the second, generated iteratively from the first, is
; the second, generated iteratively from the first, is 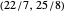 ; the third is
; the third is 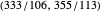 .
.
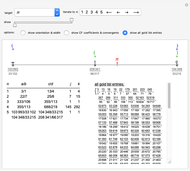
The number line plot shows the sequence of weighted mediants formed by a bracket 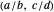 , consisting of two fractions on opposite sides of the target. The weighted mediants move monotonically from
, consisting of two fractions on opposite sides of the target. The weighted mediants move monotonically from 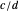 , past the target, toward
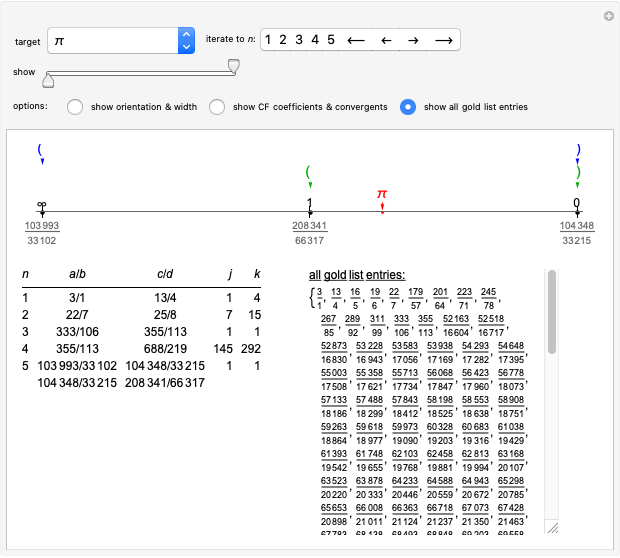
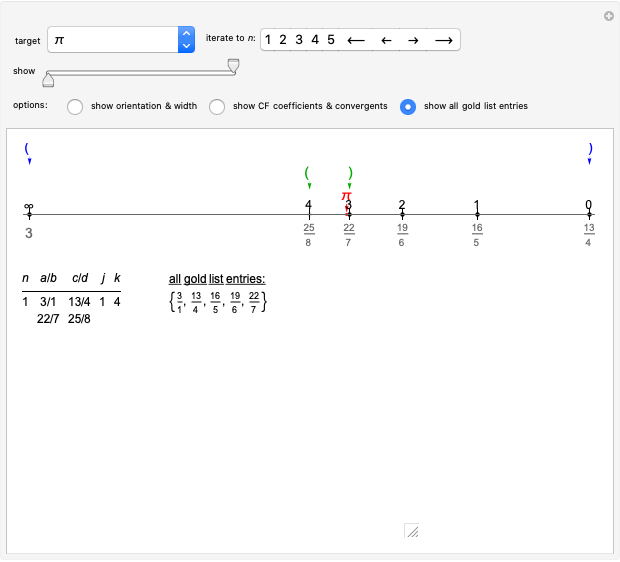
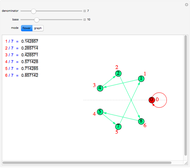
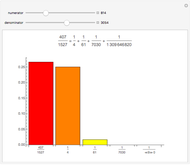
, past the target, toward 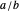 (the one with the smaller denominator). Coloring indicates which are in the gold list, and arrows show which two are closest to the target, bracketing it more closely. Below the number line, on the left, a table provides information regarding each iterative bracket; and on the right, optionally, you can choose to display either newly added elements of the gold list or the entire gold list.
(the one with the smaller denominator). Coloring indicates which are in the gold list, and arrows show which two are closest to the target, bracketing it more closely. Below the number line, on the left, a table provides information regarding each iterative bracket; and on the right, optionally, you can choose to display either newly added elements of the gold list or the entire gold list.
Snapshot 1: The first bracket of approximants of  ,
, 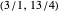 , together with calculated values of
, together with calculated values of 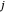 and
and  , allowing identification of
, allowing identification of 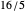 ,
, 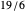 and
and 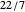 (weighted mediants with weight factors
(weighted mediants with weight factors  ,
, 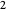 and
and 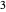 ) as three additional gold list elements. On the number line, the current and next brackets are identified by parentheses symbols, colored blue or green, respectively. The target is identified by the red point and arrow.
) as three additional gold list elements. On the number line, the current and next brackets are identified by parentheses symbols, colored blue or green, respectively. The target is identified by the red point and arrow.
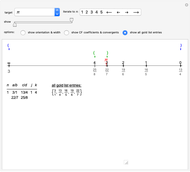
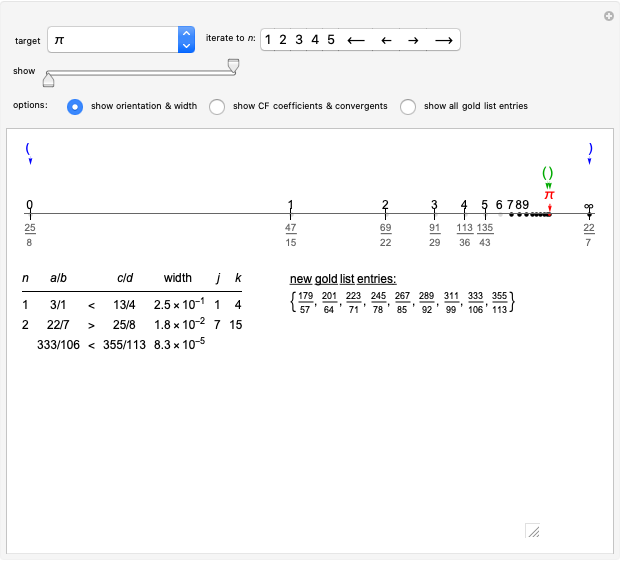
Snapshot 2: The second bracket of approximants of 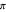 ,
, 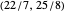 , together with calculated values of
, together with calculated values of 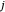 and
and  , allowing identification of 10 additional gold list elements, including the well-known "Chinese estimate" of
, allowing identification of 10 additional gold list elements, including the well-known "Chinese estimate" of 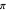 ,
, 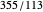 . The first six weighted mediants, shown in gray, although approaching
. The first six weighted mediants, shown in gray, although approaching 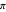 , are farther from it than
, are farther from it than 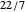 , and are therefore not in the gold list. Adjust the interval sliders to focus on later weighted mediants. In the table of bracket information, bracket width is shown to be rapidly decreasing.
, and are therefore not in the gold list. Adjust the interval sliders to focus on later weighted mediants. In the table of bracket information, bracket width is shown to be rapidly decreasing.
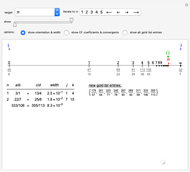
Snapshot 3: Step 6 in the iterative bracket method with target 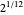 , a case of intermittent approach, some steps dividing the bracket width by 2, some far more. Continued fraction coefficients and convergents are shown.
, a case of intermittent approach, some steps dividing the bracket width by 2, some far more. Continued fraction coefficients and convergents are shown.
Snapshot 4: Step 15 in the iterative bracket method applied to the golden ratio, the case of slowest approach, with each step dividing the bracket width by slightly more than 2. Here 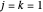 , allowing the addition of only one new gold list entry at each step.
, allowing the addition of only one new gold list entry at each step.
Iterative bracket algorithm, for a target  :
:
In the following, let 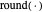 and
and 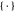 be the functions for rounding and taking the fractional part; let
be the functions for rounding and taking the fractional part; let 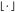 and
and  be the floor and ceiling functions.
be the floor and ceiling functions.
1. The earlier element 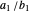 of the initial bracket, is
of the initial bracket, is 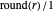 . The later element
. The later element 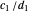 is the first approximant on the other side of
is the first approximant on the other side of  . So by definition,
. So by definition,  lies between the bracket elements. Write the bracket as
lies between the bracket elements. Write the bracket as 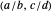 , listing first the earlier element, which has the the smaller denominator.
, listing first the earlier element, which has the the smaller denominator.
2. For any bracket 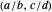 , define
, define 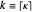 , where
, where 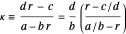 . The next bracket consists of the
. The next bracket consists of the 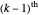 and
and 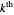 repeated mediants of the current bracket, that is,
repeated mediants of the current bracket, that is, 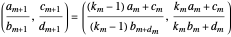 . Each successive iteration more tightly brackets the target, generally decreasing the bracket width by at least a factor of 2, often much more. Note: After
. Each successive iteration more tightly brackets the target, generally decreasing the bracket width by at least a factor of 2, often much more. Note: After 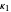 is found, all further ones can also be generated iteratively by an equivalent condition:
is found, all further ones can also be generated iteratively by an equivalent condition: 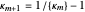 . (This is reminiscent of the way continued fraction coefficients are found.)
. (This is reminiscent of the way continued fraction coefficients are found.)
3. For any bracket, define 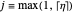 , where
, where 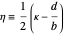 . All weighted mediants between the
. All weighted mediants between the 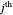 and the
and the 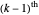 are automatically in the gold list. In addition, the
are automatically in the gold list. In addition, the 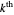 mediant of the current bracket (which becomes the later element of the next bracket,
mediant of the current bracket (which becomes the later element of the next bracket, 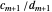 ) is in the gold list if and only if
) is in the gold list if and only if 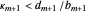 . These steps are sufficient to generate the entire gold list for any arbitrary target
. These steps are sufficient to generate the entire gold list for any arbitrary target  .
.
An interesting side note: The  -sequence generated as part of the iteration process specified above becomes identical (after at most two terms) to the continued fraction coefficients for all targets considered. A column showing the beginning of the continued fraction representation can be toggled on/off, and with it the sequence of convergents. These convergents, which are rational truncations of the continued fraction, closely mirror the sequence of
-sequence generated as part of the iteration process specified above becomes identical (after at most two terms) to the continued fraction coefficients for all targets considered. A column showing the beginning of the continued fraction representation can be toggled on/off, and with it the sequence of convergents. These convergents, which are rational truncations of the continued fraction, closely mirror the sequence of 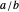 entries from the iterative bracket algorithm.
entries from the iterative bracket algorithm.
Other Demonstrations dealing with mediants and gold list approximants are listed under "Related Links". See [1] for a derivation of the algorithm, proofs of these statements and a comparison of the ultra-rapid iterative bracket method with the painfully slow 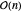 method based on the gold list definition: test each approximant and discard or save. A similar approach, considered in [2], uses lower and upper rational bounds to bracket the values of logarithms.
method based on the gold list definition: test each approximant and discard or save. A similar approach, considered in [2], uses lower and upper rational bounds to bracket the values of logarithms.
Reference
[1] R. L. Caviness and K. E. Caviness, Making Pi(e) from Scratch, Rapidly and Memorably [Video]. AMATYC Webinar (Sep 27, 2019) www.youtube.com/watch?v=JcBr_v-n6AA.
[2] T. Apostol and M. Mnatsakanian, "Good Rational Approximations to Logarithms," College Mathematics Journal, 32(3), 2001 pp. 172–179. https://doi.org/10.1080/07468342.2001.11921872.
Permanent Citation