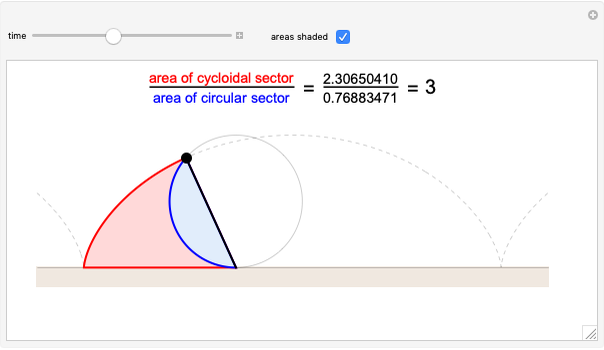
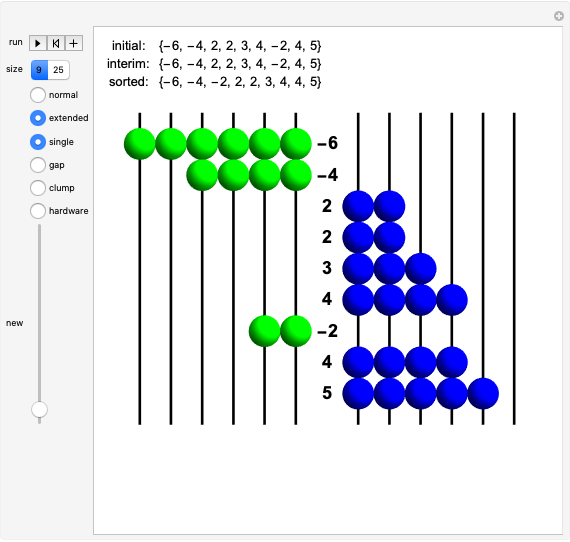
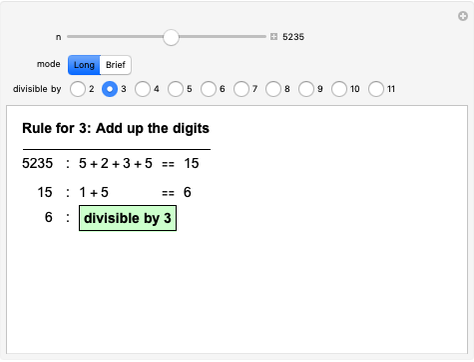
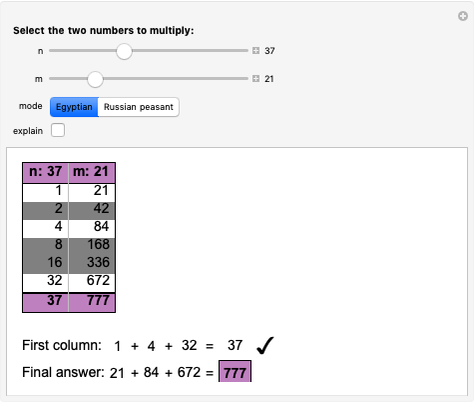
Calkin-Wilf Tree of Fractions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
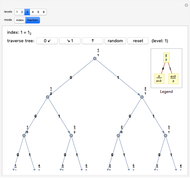
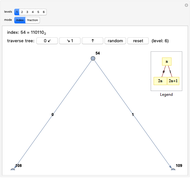
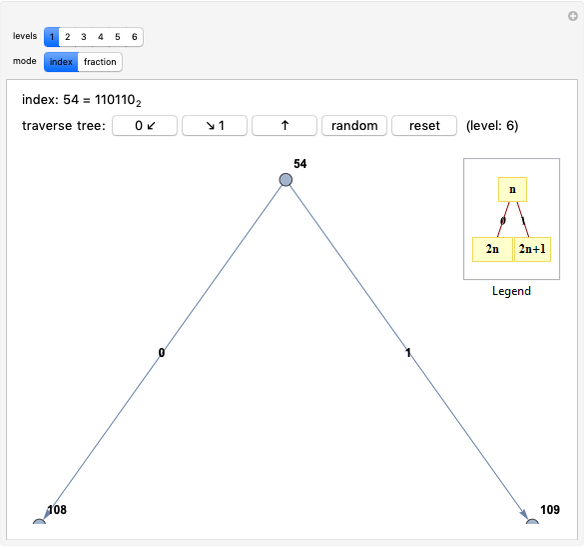
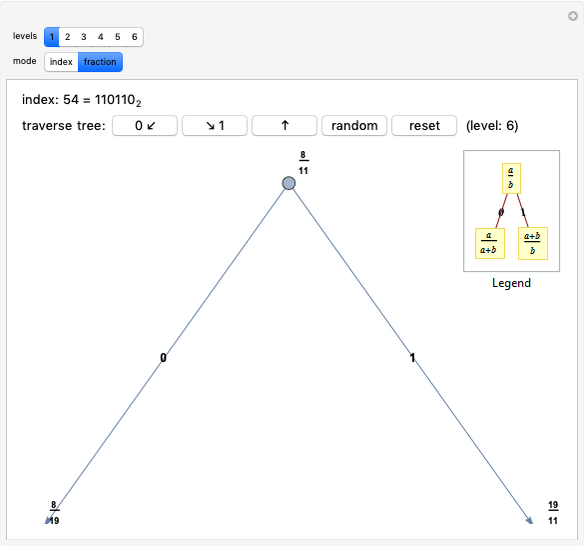
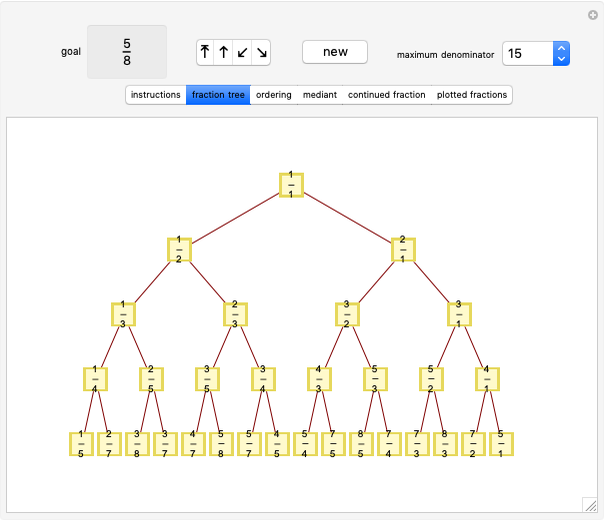
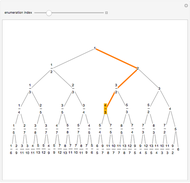
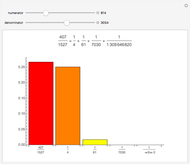
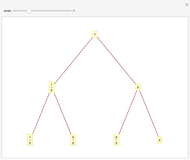
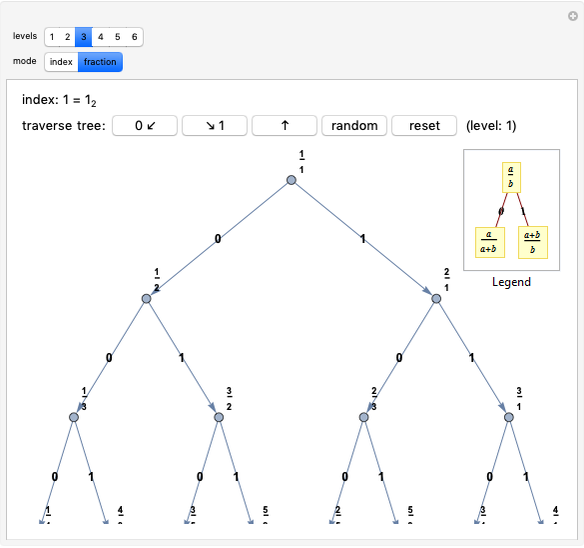
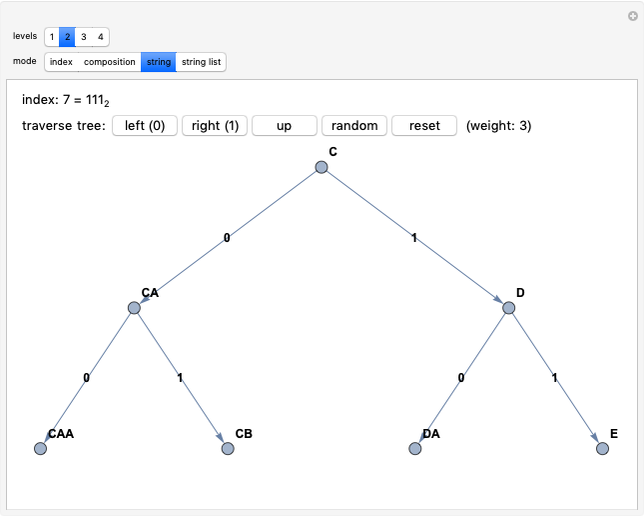
The Calkin–Wilf tree contains all positive fractions in reduced form. Click the buttons to move down to the left or right, or to move up. The fraction's index is shown in decimal and binary notation to highlight the connections between the binary expansion of the index and the fraction's position in the tree.
Contributed by: Kenneth E. Caviness (May 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The rank (or index) assigned to a fraction can be thought of as its address in the Calkin–Wilf tree. Since the tree is binary, you can move from one node to another in three ways: down to the left child node or right child node, or up to the parent node. You can also move to a randomly selected point in the tree or reset the visible part of the tree to the root position.
In fraction mode, the left button adds the numerator to the denominator and the right button adds the denominator to the numerator (leaving the other unchanged in both cases), while the up button replaces the larger of the two by their difference.
In index mode, the left and right children of node  have indices
have indices  and
and  , respectively. Both modes show the binary representation of the index code of the node at the top of the displayed subtree, starting with a 1 and continuing with precisely the bits (0 or 1) indicated by pushing the buttons. The bits of the index thus provide a "breadcrumb trail" for the path down the tree. Moving back up the tree corresponds to lopping off the last bit, or dividing the index by 2, discarding the remainder.
, respectively. Both modes show the binary representation of the index code of the node at the top of the displayed subtree, starting with a 1 and continuing with precisely the bits (0 or 1) indicated by pushing the buttons. The bits of the index thus provide a "breadcrumb trail" for the path down the tree. Moving back up the tree corresponds to lopping off the last bit, or dividing the index by 2, discarding the remainder.
The Calkin–Wilf enumeration provides a one-to-one mapping of the positive rationals onto the positive integers, thus demonstrating that the set of rational numbers is countably infinite. The Stern–Brocot tree gives an alternative, related enumeration.
Reference
[1] N. Calkin and H. S. Wilf, "Recounting the Rationals," The American Mathematical Monthly, 107(4), 2000 pp. 360–363.
Permanent Citation