Representation of Spinors by Two-Dimensional Complex Rotations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
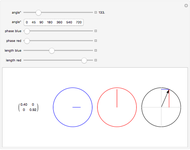
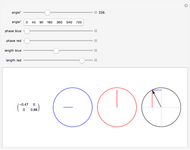
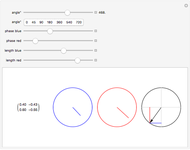
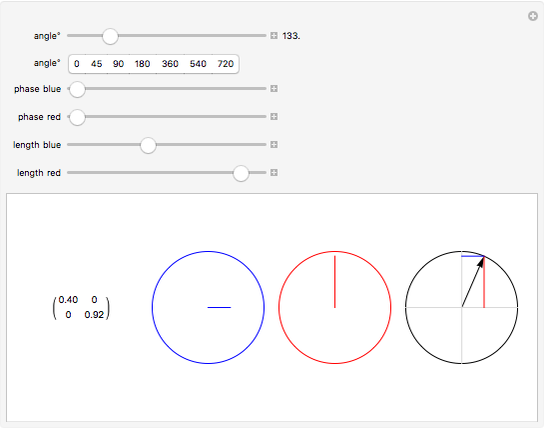
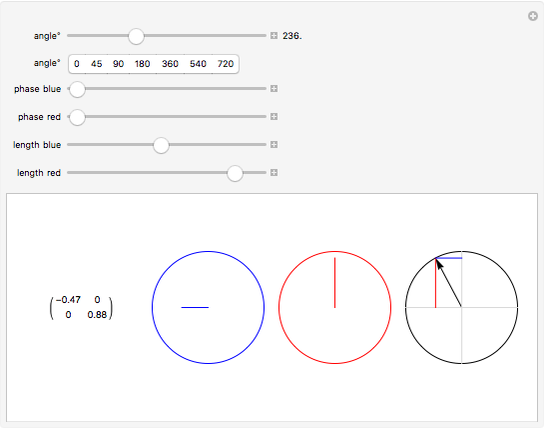
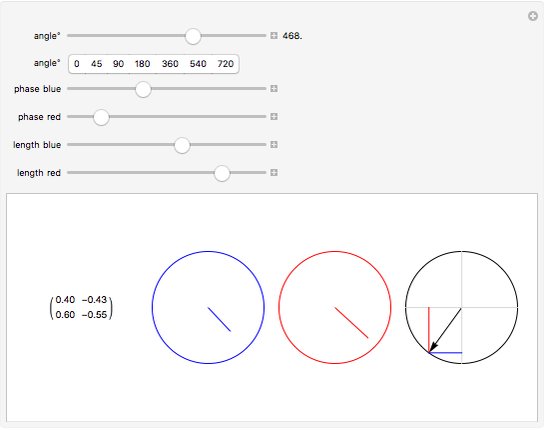
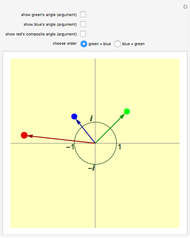
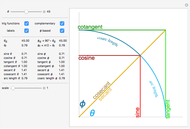
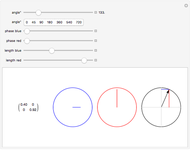
This Demonstration shows rotation in two complex dimensions and how this can represent a spinor. The matrix on the left shows the action of a spinor transform of the given angle on a unit vector. Remember that this is a unit vector in 2D complex space, so it has two complex components that can be represented by a two-row vector. The two circles on the left are graphical representations of these complex components. The circle at the far right shows the length of each complex component as one of the projections of a unit vector in the 2D real plane. This circle represents the constraints on the values of the complex components. Each component may have a different value, but the sum of the squares of their two lengths must equal 1.
[more]
Contributed by: Ted Frazier (February 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The directions of the complex numbers and constraint have no simple relation to real directions in space. Just as every point in space can have a temperature, a single quantity, there are some qualities that a point in space can have that require a more complex description than a single number. A quantum wave function (a Pauli 2-spinor) is like this, where every point in space can be represented by two complex numbers under the above constraint. These directions are represented in an abstract four-dimensional space.
For a 2D real rotation on a unit vector, there is a similar constraint. The squares of the lengths of the projections of the vector onto the  and
and 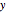 axes must sum to 1. The 2D complex rotation has the same constraint except the projections are now the lengths of the two underlying complex components. If either of these lengths change, the other must also to keep the constraint valid. These two complex numbers can also change independently via a change of phase, which does not change their length. This phase change is what gives 2D complex rotation more degrees of freedom than a 2D real rotation. It can exhibit behavior similar to a 2D real rotation, but it can also change its underlying components in more ways than a real rotation.
axes must sum to 1. The 2D complex rotation has the same constraint except the projections are now the lengths of the two underlying complex components. If either of these lengths change, the other must also to keep the constraint valid. These two complex numbers can also change independently via a change of phase, which does not change their length. This phase change is what gives 2D complex rotation more degrees of freedom than a 2D real rotation. It can exhibit behavior similar to a 2D real rotation, but it can also change its underlying components in more ways than a real rotation.
References
B. A. Schumm, Deep Down Things: The Breathtaking Beauty of Particle Physics, Baltimore, MD: Johns Hopkins University Press, 2004.
G. Arfken, Mathematical Methods for Physicists, 3rd ed., Orlando, FL: Academic Press, 1985.
Permanent Citation
"Representation of Spinors by Two-Dimensional Complex Rotations"
http://demonstrations.wolfram.com/RepresentationOfSpinorsByTwoDimensionalComplexRotations/
Wolfram Demonstrations Project
Published: February 20 2012