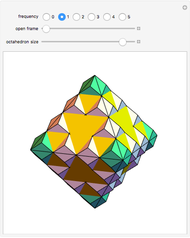
Rhombic Hexecontahedron in a Rhombohedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
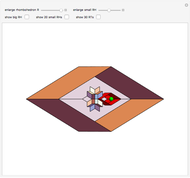
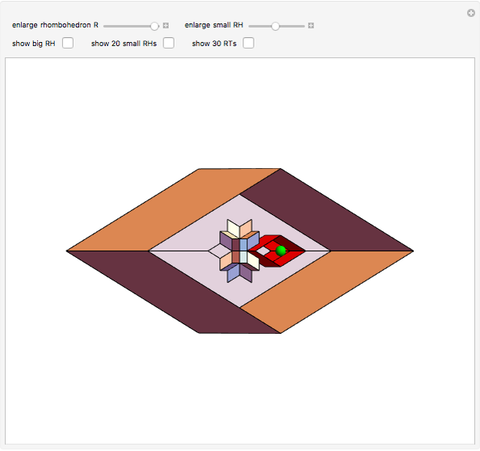
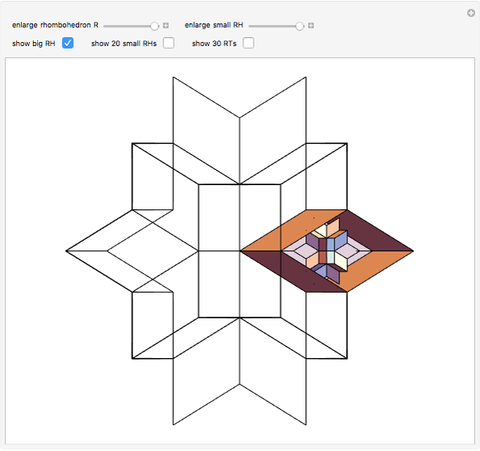
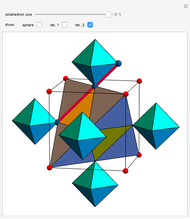
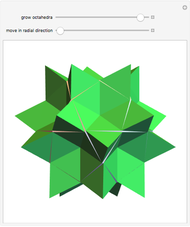
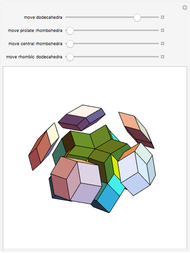
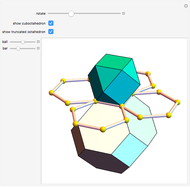
Find a point that divides the diagonal of a large rhombohedron  in proportion to the golden ratio. Construct a small rhombohedron
in proportion to the golden ratio. Construct a small rhombohedron  around this point so that one of its vertices coincides with the center of
around this point so that one of its vertices coincides with the center of  . Construct a rhombic hexecontahedron
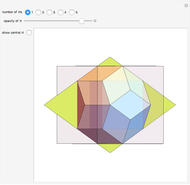
. Construct a rhombic hexecontahedron  so that one of its constituent 20 rhombohedra coincides with
so that one of its constituent 20 rhombohedra coincides with  . If you enlarge the
. If you enlarge the  , then you will see two small dots on each face of
, then you will see two small dots on each face of  , which are actually vertices of the
, which are actually vertices of the  . (Drag to rotate the graphic to see the dots.) Therefore,
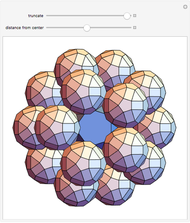
. (Drag to rotate the graphic to see the dots.) Therefore,  vertices (out of 20) of the
vertices (out of 20) of the  are on the six faces of
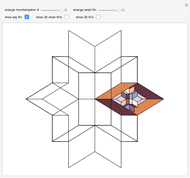
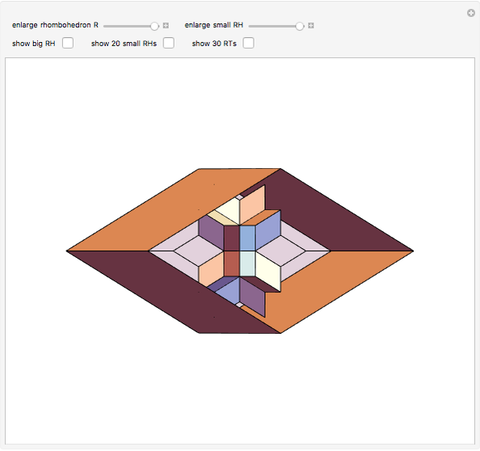
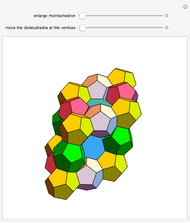
are on the six faces of  . When 20 rhombohedra with
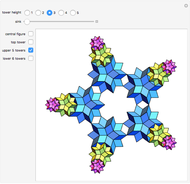
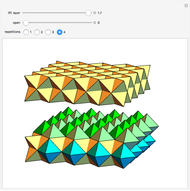
. When 20 rhombohedra with  s inside them are assembled to form a large
s inside them are assembled to form a large  , then the
, then the  s meet at their vertices, and a rhombic triacontahedron connected face-to-face can be inserted between them.
s meet at their vertices, and a rhombic triacontahedron connected face-to-face can be inserted between them.
Contributed by: Sándor Kabai (October 2015)
With additional contribution by: István Muzsai
Open content licensed under CC BY-NC-SA
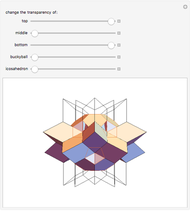
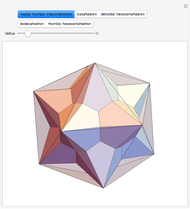
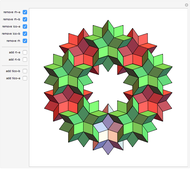
Snapshots
Details
detailSectionParagraphPermanent Citation
"Rhombic Hexecontahedron in a Rhombohedron"
http://demonstrations.wolfram.com/RhombicHexecontahedronInARhombohedron/
Wolfram Demonstrations Project
Published: October 28 2015