Riemann's Almost Nowhere Differentiable Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In the late nineteenth century, Riemann proposed the function  as an example of a continuous function that is almost nowhere differentiable. This Demonstration shows the graphs of generalized versions of Riemann's function, defined by
as an example of a continuous function that is almost nowhere differentiable. This Demonstration shows the graphs of generalized versions of Riemann's function, defined by  , where
, where  and
and  are real parameters satisfying
are real parameters satisfying  and
and  , and corresponding functions are obtained by replacing
, and corresponding functions are obtained by replacing  by
by  or
or  .
.
Contributed by: Saurav Chittal, Malachi Robinson, Manisha Garg and A. J. Hildebrand.
(Based on an undergraduate research project at the Illinois Geometry Lab in Fall 2022.) (June 13)
Open content licensed under CC BY-NC-SA
Details
Given two real parameters  and
and  , the generalized complex Riemann function is defined as
, the generalized complex Riemann function is defined as
 .
.
The generalized Riemann sine and cosine functions are defined as the imaginary and real parts of  , respectively:
, respectively:
 ,
,

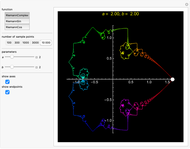
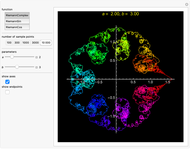
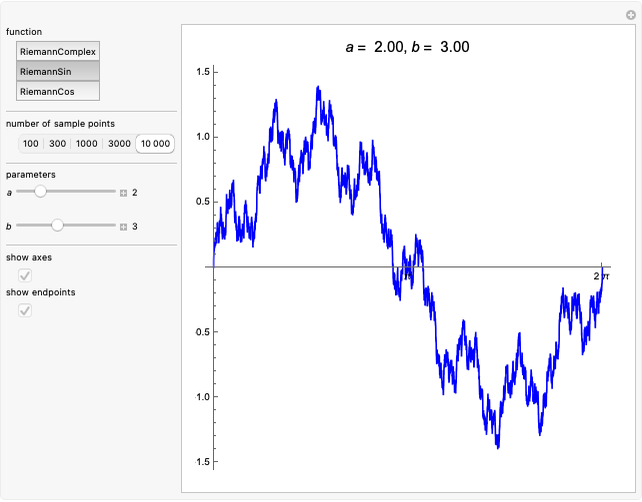
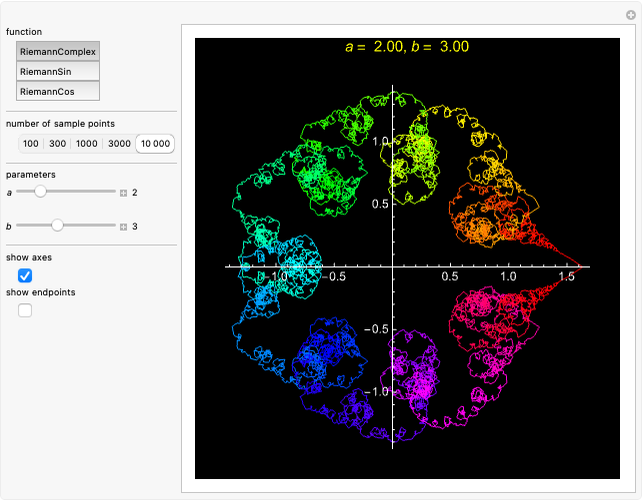
All three types of Riemann functions are known to be continuous but almost nowhere differentiable, and their graphs exhibit fractal behavior [1–3].
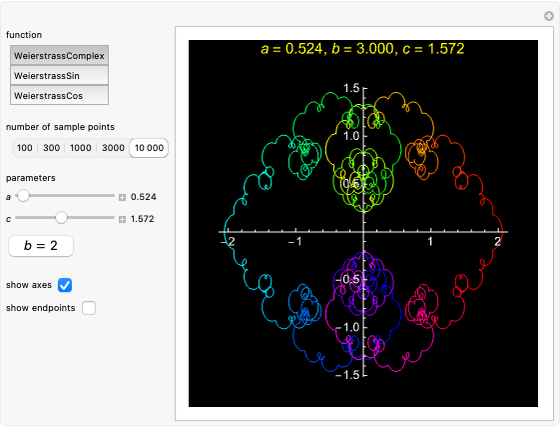
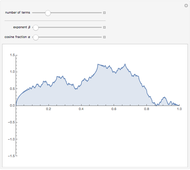
This Demonstration shows the graphs of the real-valued Riemann sine and cosine functions,  and
and  , over the interval
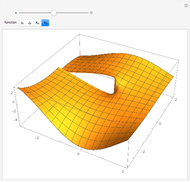
, over the interval  , and the graph of the complex Riemann function,
, and the graph of the complex Riemann function,  ,
,  , represented by a path in the complex plane. In the case when
, represented by a path in the complex plane. In the case when  is an integer, the function
is an integer, the function  is periodic with period 1, so the corresponding path is closed.
is periodic with period 1, so the corresponding path is closed.
References
[1] F. Chamizo and A. Córdoba, "Differentiability and Dimension of Some Fractal Fourier Series," Advances in Mathematics, 142(2), 1999 pp. 335–354. doi:10.1006/aima.1998.1792.
[2] J. J. Duistermaat, "Selfsimilarity of 'Riemann's Nondifferentiable Function'," Nieuw Archief voor Wiskunde, 9(3), 1991 pp. 303–337. https://dspace.library.uu.nl/handle/1874/2601.
[3] J. Gerver, "More on the Differentiability of the Riemann Function," American Journal of Mathematics, 93(1), 1971 pp. 33–41. doi:10.2307/2373445.
Snapshots
Permanent Citation