Rotational Symmetry of Multivariate Uncorrelated Standard Normal Distribution

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
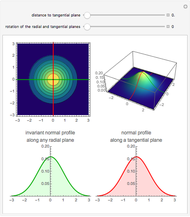
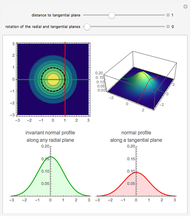
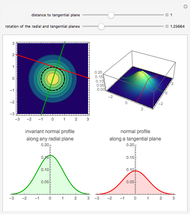
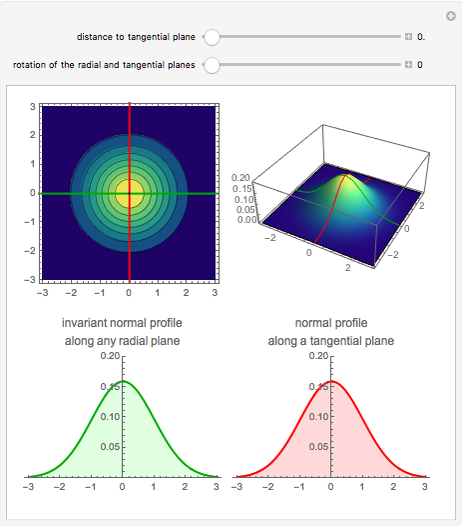
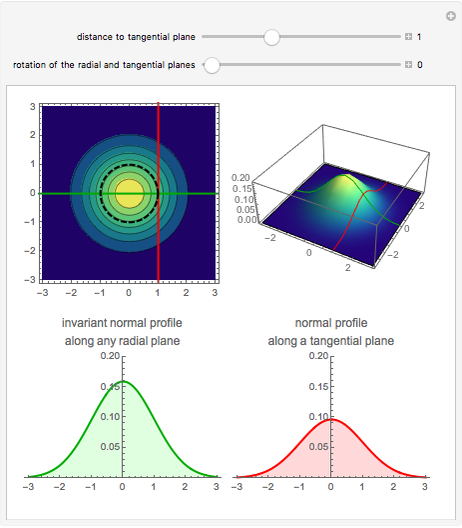
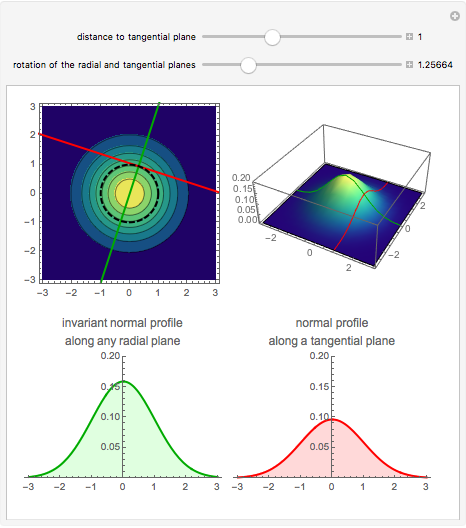
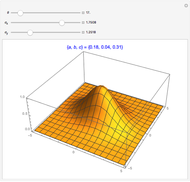
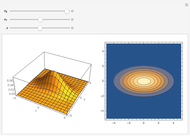
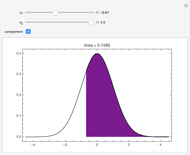
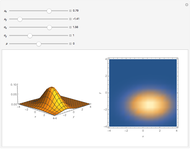
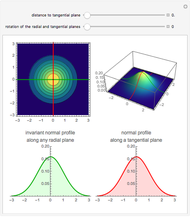
Rotational symmetry is a key property of the multivariate uncorrelated standard normal distribution. The top part of this Demonstration displays the contour and the 3D plots of a bivariate uncorrelated standard normal distribution. Both plots are intersected by two vertical planes or half-spaces. The radial plane runs through the origin and the tangential plane is perpendicular to it at a variable distance. The bottom parts display the density profiles created by the intersections. These profiles are standard normals up to a normalizing constant.
Contributed by: Diego M. Oviedo-Salcedo (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Notice that the density profile on the lower-left plane remains unchanged for any direction of the radial plane, whereas the profile corresponding to the tangential plane diminishes as the plane moves away from the origin. However, the latter profile is the same for a plane at a given distance from the origin.
This property is useful when performing risk quantification using reliability analysis of systems involving more than one correlated random variable. The original variates are transformed into the uncorrelated standard normal space and the probability of failure is computed with the help of the transformed space.