Maximum Likelihood Estimators with Normally Distributed Error

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
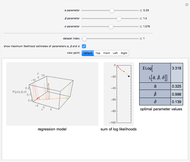
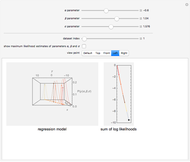
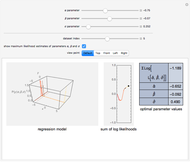
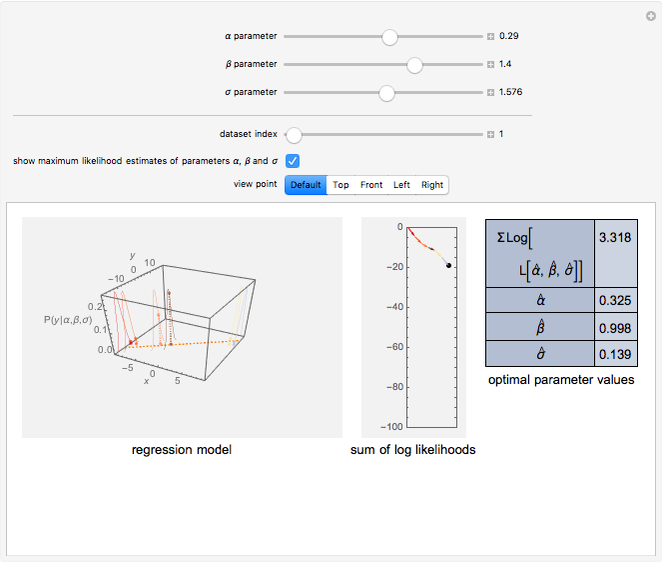
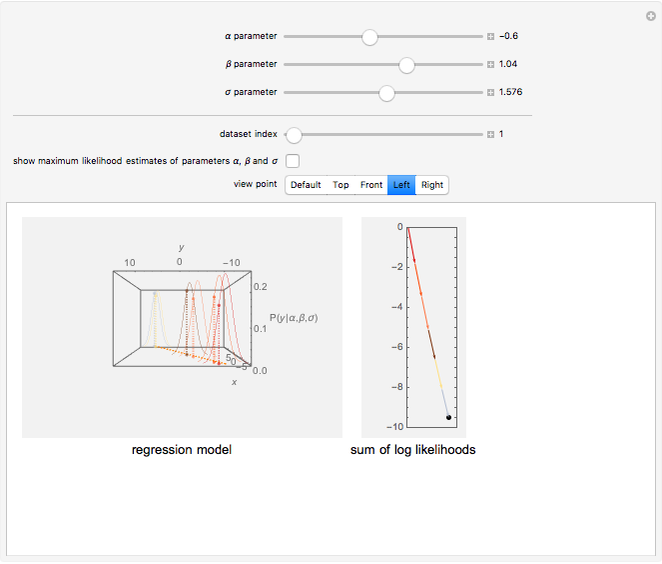
In statistics, there is a frequent desire to develop a model that has, of all models in that class, the maximum likelihood of producing the data observed. This Demonstration shows how to derive the maximum likelihood estimates of the coefficients in a linear model of data ( ) that is believed to have normally distributed error with a standard deviation of a user-set value
) that is believed to have normally distributed error with a standard deviation of a user-set value  . The top panel shows the data, the current regression model (as an orange line) and the probability (likelihood) that each
. The top panel shows the data, the current regression model (as an orange line) and the probability (likelihood) that each  value would occur for a given
value would occur for a given  value, given
value, given  and
and  . The bottom panel shows the sum of the logs of each of these likelihoods. Selection of maximum likelihood estimates of
. The bottom panel shows the sum of the logs of each of these likelihoods. Selection of maximum likelihood estimates of  and
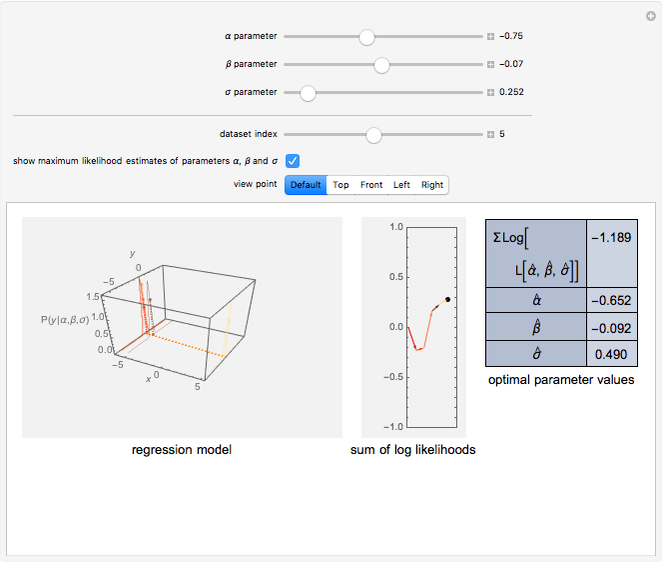
and  will make this sum as large as possible and the displayed rectangle as small as possible. Curious users can request a computation of the maximum likelihood estimate for each dataset.
will make this sum as large as possible and the displayed rectangle as small as possible. Curious users can request a computation of the maximum likelihood estimate for each dataset.
Contributed by: Seth J. Chandler (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For pedagogical purposes, this Demonstration finds maximum likelihood estimators using a general approach. In specific cases, more efficient and swifter computational methods may exist. In particular, optimal parameter values in the case of normally distributed error can be obtained via linear least-squares optimization; the maximum likelihood estimate of the standard deviation can be obtained as the square root of the mean of the squared residuals. The code underlying this Demonstration permits this swifter but less general methodology to be used.
This Demonstration will be more responsive to movements of the parameter sliders if no computation of the maximum likelihood estimate is requested.
A useful experiment is to set the parameter sliders so that they correspond to the optimal parameter values determined by the computer. Then determine the effect on the sum of the log likelihoods as the σ parameter increases. Then see what happens if you set the α and β parameter sliders to suboptimal levels. Does increasing  increase or decrease the sum of the log likelihoods?
increase or decrease the sum of the log likelihoods?
Permanent Citation