Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Saturday Morning Breakfast Cereal Fourier Transform

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

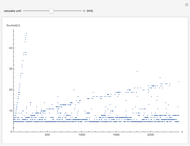
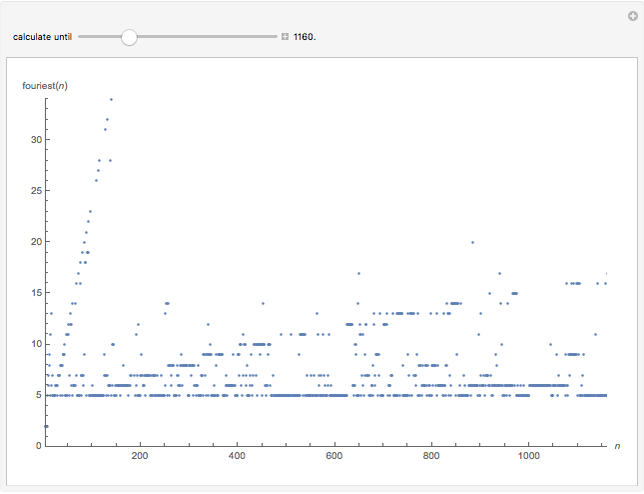
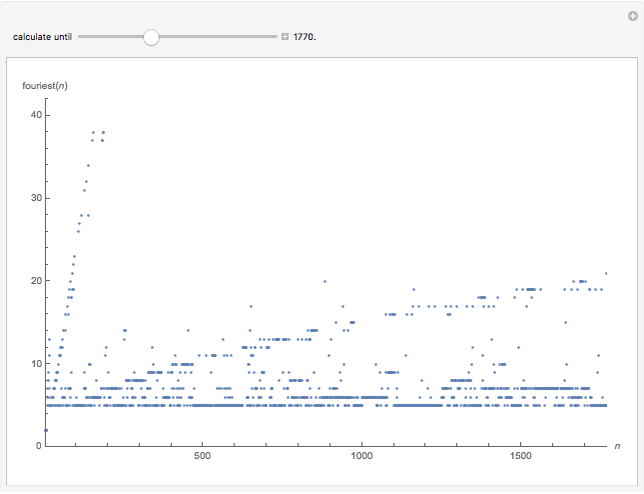
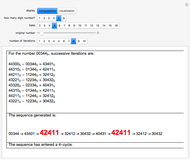
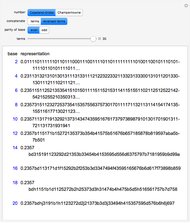
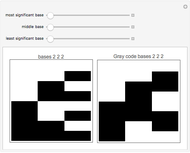
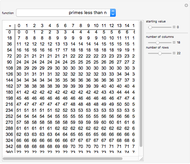
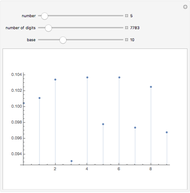
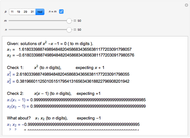
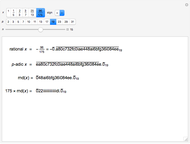
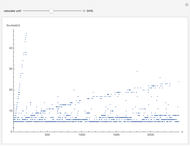
Given an integer , there is a smallest base for which the number has the most fours in its representations among all bases. Consider the function that gives such a base for .

[more]

Saturday Morning Breakfast Cereal calls this the "fouriest base" [1], and considers the act of moving from one base to another with more fours to be a "fourier transform".

This Demonstration calculates the fouriest base for all numbers less than a certain limit. Often is the fouriest base for .

[less]

Contributed by: Robert Spencer (September 2016)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] Z. Weinersmith, Saturday Morning Breakfast Cereal (blog). (Sep 8, 2016) www.smbc-comics.com/index.php?db=comics&id=2874#comic.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send