Golden Integers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
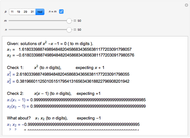
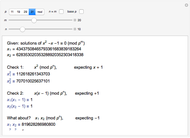
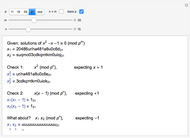
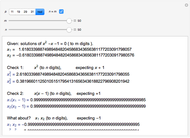
The positive root of the golden polynomial  is the famous golden ratio
is the famous golden ratio  and the negative root is
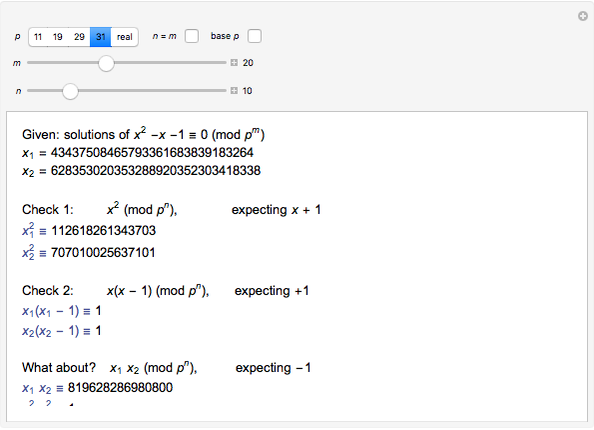
and the negative root is  . There are two integer solutions
. There are two integer solutions  and
and  to the congruence
to the congruence  , where
, where  is a prime and
is a prime and  is a positive integer (in this Demonstration,
is a positive integer (in this Demonstration,  and
and  ). Can either
). Can either  or
or  be called a "golden integer" that is analogous to
be called a "golden integer" that is analogous to  ?
?
Contributed by: Robert L Brown (March 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
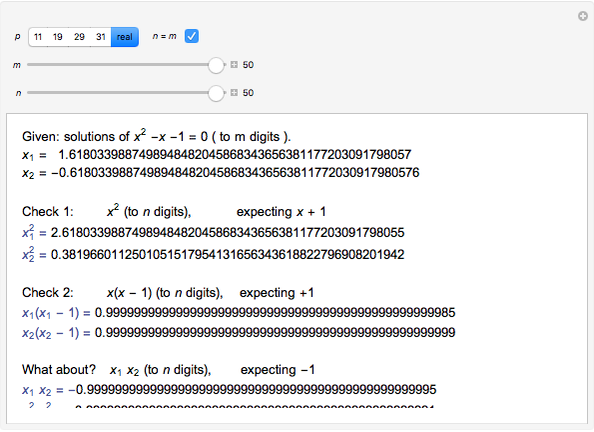
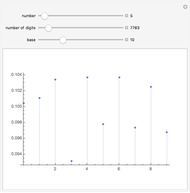
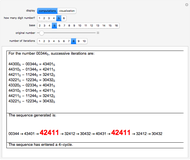
Kurt Hensel (1861–1941) discovered that for certain prime numbers  , there are two roots to the "golden polynomial" modulo
, there are two roots to the "golden polynomial" modulo  . Further, he claimed that for each of those primes and for every natural number
. Further, he claimed that for each of those primes and for every natural number  , there would also exist two roots congruent modulo
, there would also exist two roots congruent modulo  .
.
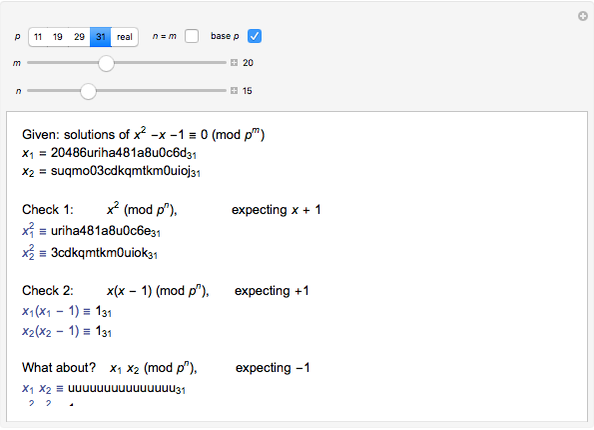
When you choose the "base  " option and vary
" option and vary  from 1 to 50, it is clear that the 50 different congruences are related. They are a single infinite sequence written as
from 1 to 50, it is clear that the 50 different congruences are related. They are a single infinite sequence written as  (base
(base  ) that is truncated on the left to leave
) that is truncated on the left to leave  significant digits
significant digits  . Likewise, the 50 checks are a single infinite integer (base
. Likewise, the 50 checks are a single infinite integer (base  ) that is truncated to
) that is truncated to  digits.
digits.
With the "base  " option set and
" option set and  , notice the strong analogy between modular arithmetic and real arithmetic as you vary
, notice the strong analogy between modular arithmetic and real arithmetic as you vary  . The infinite sequences (base
. The infinite sequences (base  ) behave like "real" infinitely repeating decimals. And like repeating decimals, the most significant digits are nearer the decimal point.
) behave like "real" infinitely repeating decimals. And like repeating decimals, the most significant digits are nearer the decimal point.
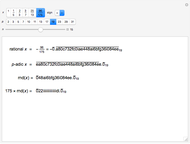
Writing the 50 congruences as a single truncated sequence (base  ) inspired the introduction of
) inspired the introduction of  -adic numbers by Kurt Hensel in 1897. Powerful applications of
-adic numbers by Kurt Hensel in 1897. Powerful applications of  -adic numbers have been found in number theory, including the famous proof of Fermat's last theorem by Andrew Wiles.
-adic numbers have been found in number theory, including the famous proof of Fermat's last theorem by Andrew Wiles.
Permanent Citation