Newton's Method in  -adic Form
-adic Form

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
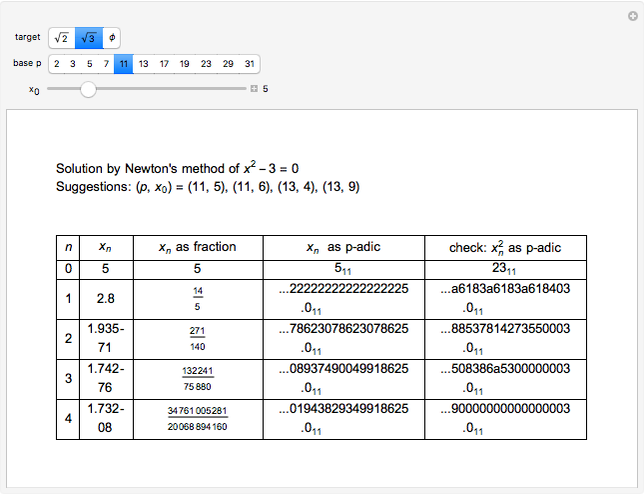
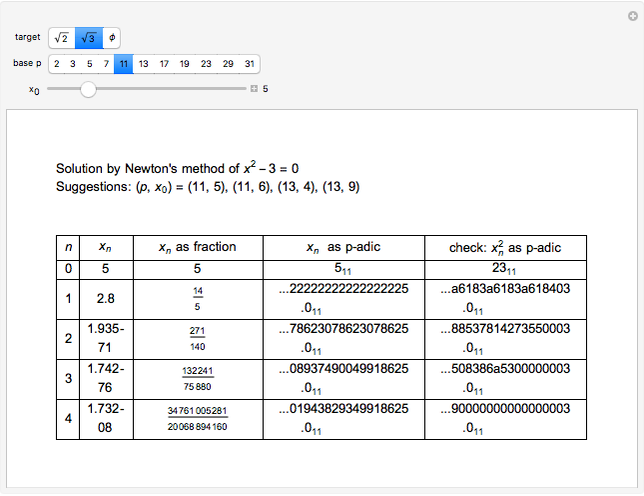
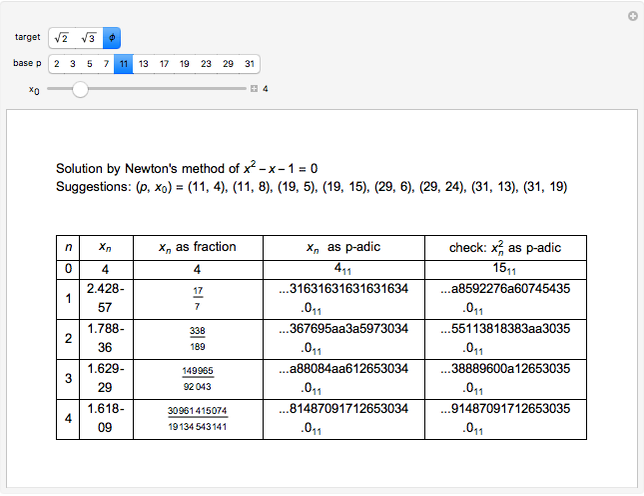
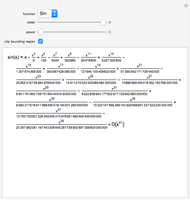
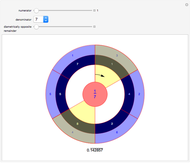
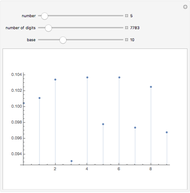
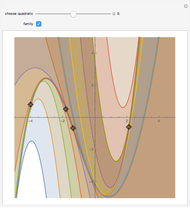
This Demonstration applies Newton's method to three polynomials with rational coefficients to approximate the irrational numbers  ,
,  , and
, and  (with these decimal approximations to 10 places:
(with these decimal approximations to 10 places:  ,
,  , and
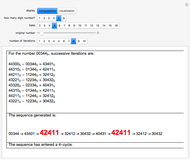
, and  ). If the iteration begins with a rational number
). If the iteration begins with a rational number  , each successive iteration is also rational as shown in column 3, with heading "
, each successive iteration is also rational as shown in column 3, with heading " as fraction".
as fraction".
Contributed by: Robert L. Brown (January 2015)
Open content licensed under CC BY-NC-SA
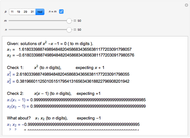
Snapshots
Details
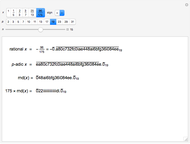
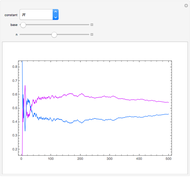
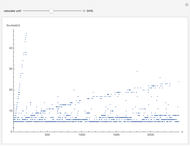
The sense in which " as
as  -adic" converges to the target irrational number is called a Cauchy sequence using a
-adic" converges to the target irrational number is called a Cauchy sequence using a  -adic norm metric. Hensel's lifting lemma [1] ensures that given a polynomial
-adic norm metric. Hensel's lifting lemma [1] ensures that given a polynomial  , if there is an integer that satisfies
, if there is an integer that satisfies  , it can be used for
, it can be used for  as
as  -adic.
-adic.
Powerful applications of  -adic numbers have been found in number theory, including the famous proof of Fermat’s last theorem by Andrew Wiles.
-adic numbers have been found in number theory, including the famous proof of Fermat’s last theorem by Andrew Wiles.
Reference
[1] K. Conrad. "Hensel's Lemma." (Nov 13, 2014) www.math.uconn.edu/~kconrad/blurbs/gradnumthy/hensel.pdf.
Permanent Citation