Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Sensitivity of Elementary Cellular Automata to Their Inputs

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

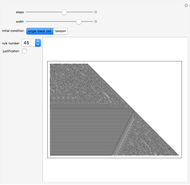
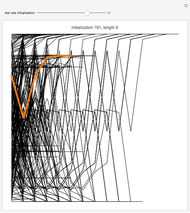
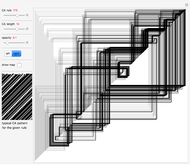
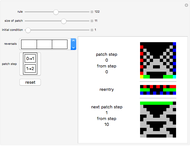
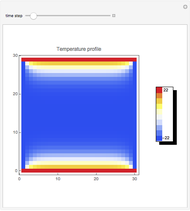
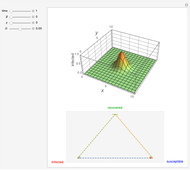
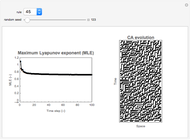
The sensitivity of an elementary cellular automaton (CA) to its inputs is defined as the space-averaged proportion of the cells in the neighborhoods of the CA's cells , that is, ), that affect the state of during the subsequent time step. This proportion can be expressed as

[more]

,

where denotes the number of cells upon which the CA is built and represents the , entry in an Jacobian matrix that can be one if a modification of the state of at the time step implies a perturbation of 's state during the subsequent time step and is zero otherwise. Since for an elementary CA, , constitutes a tridiagonal matrix and if and only if for every neighbor of , and this holds for every of the CA. It has been shown that can be employed to find an upper bound on the maximum Lyapunov exponent of elementary CA.

[less]

Contributed by: Jan Baetens (August 2011)
Open content licensed under CC BY-NC-SA

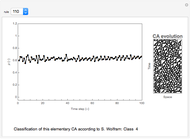
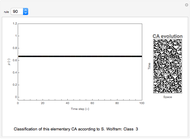
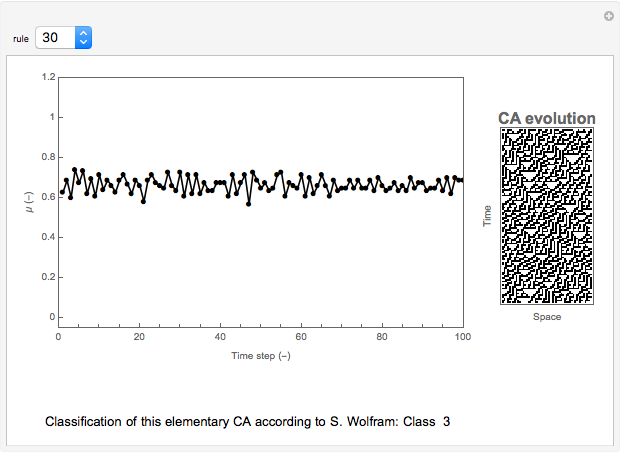
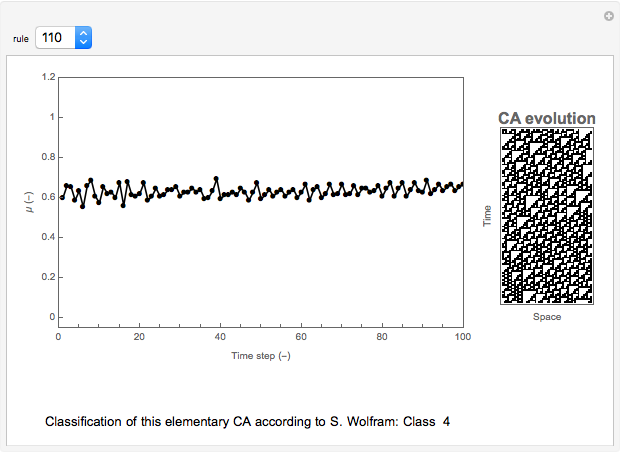
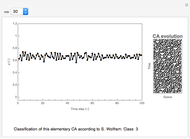
Snapshots

Details

More information on the sensitivity of CA to their inputs can be found in [1], [2], and [3].

References

[1] J. M. Baetens and B. De Baets, "Phenomenological Study of Irregular Cellular Automata Based on Lyapunov Exponents and Jacobians," Chaos, 20, 033112, 2010. doi:10.1063/1.3460362.

[2] J. M. Baetens and B. De Baets, "On the Topological Sensitivity of Sellular Automata," Chaos, in press, 2011.

[3] F. Bagnoli, R. Rechtman, and S. Ruffo, "Damage Spreading and Lyapunov Exponents in Cellular Automata," Physics Letters A, 172, pp. 34–38. doi:10.1016/0375-9601(92)90185-O.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send