Spatio-Temporal Epidemic Spread

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
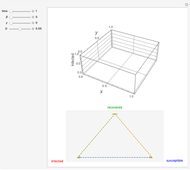
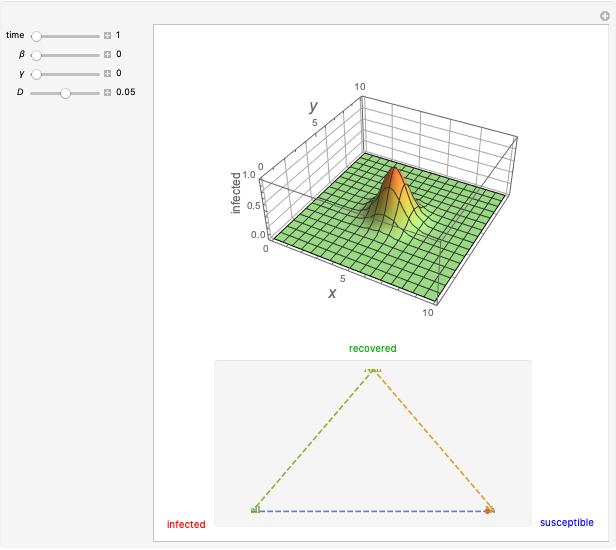
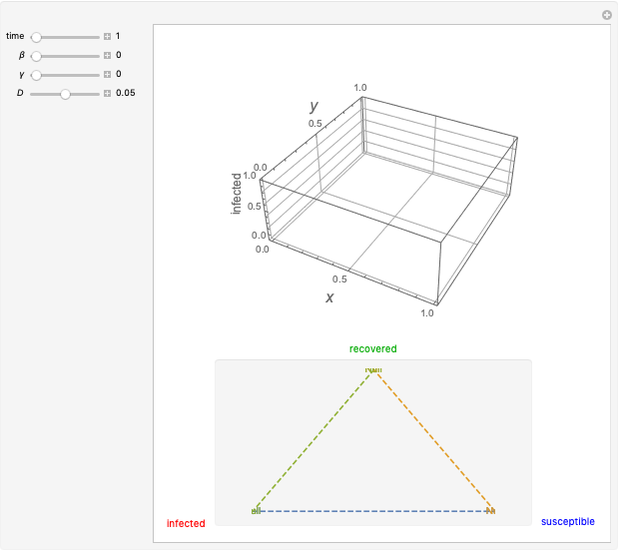
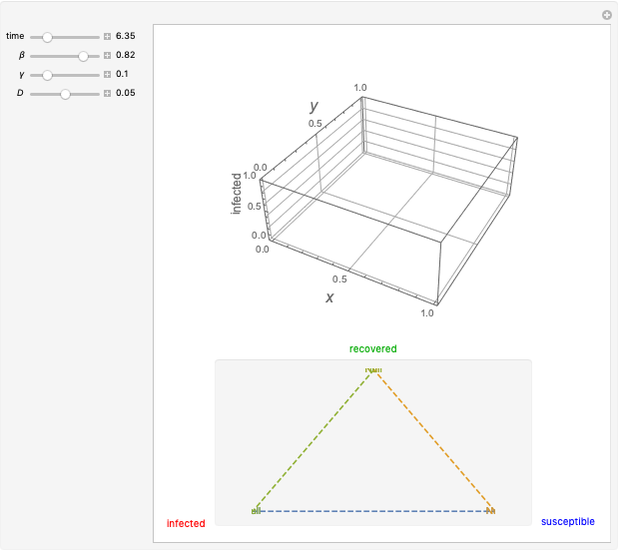
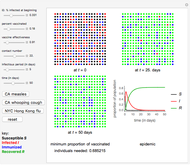
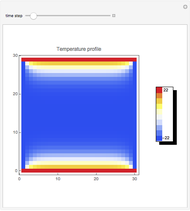
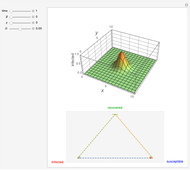
This Demonstration shows the spatio-temporal propagation of an epidemic that starts in the center of a square that contains a homogeneous population. The triangle at the bottom shows the ratio between susceptible, infected, and recovered individuals. Depending on the ratios between the contact rate 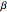 , the recovery rate
, the recovery rate  , and the mobility of the individuals
, and the mobility of the individuals  , the disease either propagates through the space or fades away. For a given instant in time, the 3D plot illustrates the proportion of infected individuals as a function of
, the disease either propagates through the space or fades away. For a given instant in time, the 3D plot illustrates the proportion of infected individuals as a function of  and
and  .
.
Contributed by: Jan Baetens (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This model is a spatial extension of the well-established SIR-type epidemiological models that account for the dispersal rate  , contact rate
, contact rate 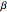 , recovery rate
, recovery rate  , and the mobility of the individuals
, and the mobility of the individuals  . As such, it provides far more realistic simulations of in natura disease outbreaks than the classical epidemiological models that have become well established since the work of Kermack and McKendrick (1927). The model equations are given by:
. As such, it provides far more realistic simulations of in natura disease outbreaks than the classical epidemiological models that have become well established since the work of Kermack and McKendrick (1927). The model equations are given by:



Snapshots 1–4 show the spatio-temporal evolution of the proportion of infected individuals for a parameter setting that allows the epidemic wave to propagate across the region.
References
[1] W. O. Kermack and A. G. McKendrick, "A Contribution to the Mathematical Theory of Epidemics," Proceedings of the Royal Society London A, 115(772), 1927 pp. 700–721. dx.doi.org/doi:10.1098/rspa.1927.0118.
[2] J. D. Murray, Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd ed., Berlin: Springer, 2003.
Permanent Citation