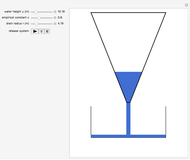
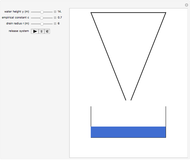
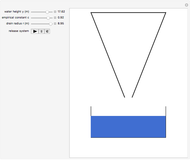
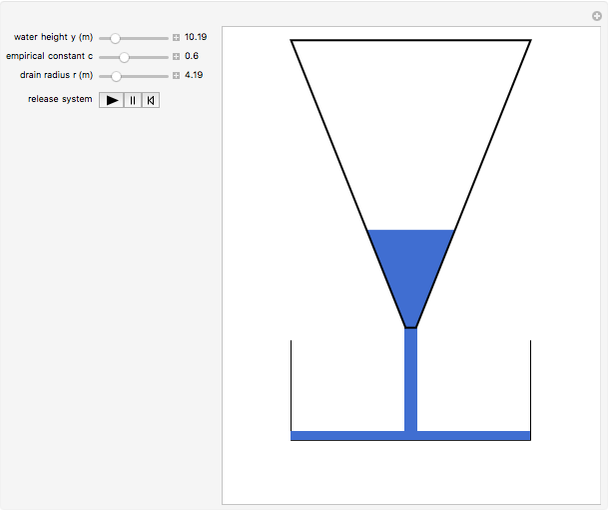
Torricelli's Law for Tank Draining
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
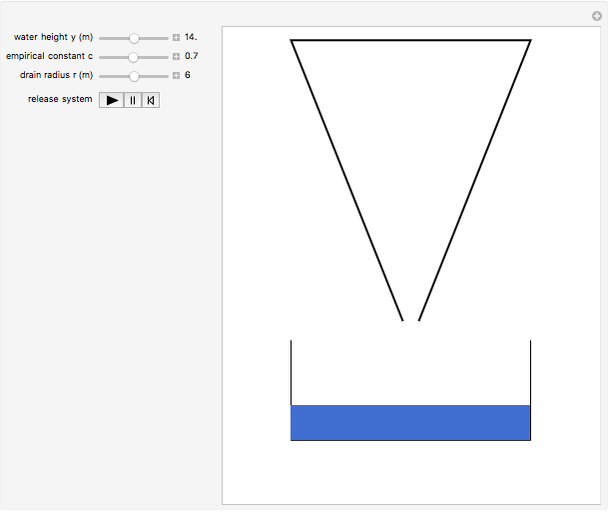
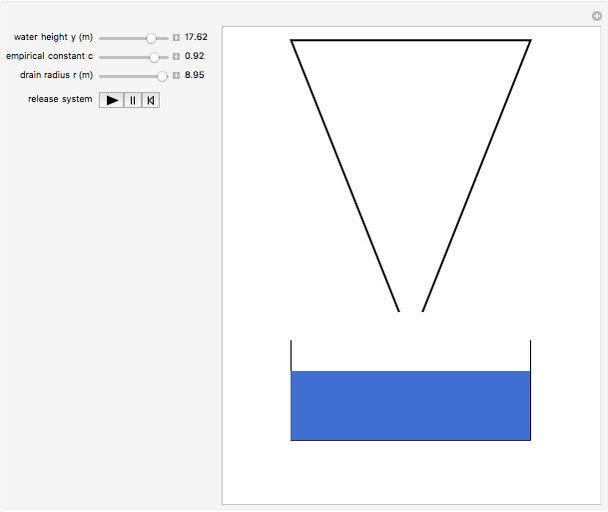
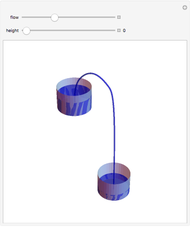
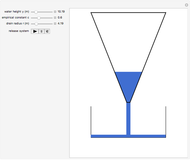
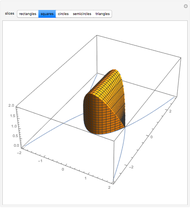
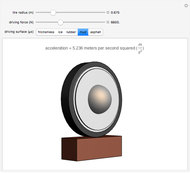
A liquid flows out of the bottom of a funnel. By Torricelli's law, the velocity of the liquid at the outlet is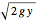 
, where 
is the acceleration due to gravity and 
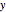is the depth of the liquid. The flow is then 
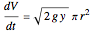, where 
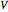is the volume and 
is the radius of the drain.
Contributed by: Stephen Wilkerson and Mark Evans (Towson University) (March 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
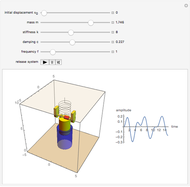
The differential equation for 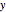, the depth of the water (in feet), is 
, where the empirical constant 
can be set to compensate for viscosity and turbulence, is the drain radius (inches),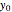 
is the initial height of the water, and 
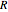is the radius of the top of the cone.
The final time is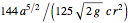 
.
The volume of the cone is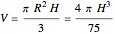 
, where 
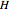is the height of the cone, and 
=
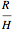for this Demonstration.
The volume of the tank is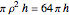 
, where 
is the radius of the tank and 
is its height.
At any time the height of the water in the drain tank can be found by: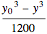 
.
The volume of the drain tank is exactly the same as the cone when it is filled to the top.
Permanent Citation
Time to Drain a Tank Using Torricelli's Law
Ed O'Grady
Flow of Fluid through a Hole in a Tank
Rana Gordji and Sam Gordji
Green's Functions for Diffusion
Brian Vick
Floating Ball
Vincent Shatlock and Autar Kaw
The Principle of Archimedes
Enrique Zeleny
Action of a Siphon
Enrique Zeleny
Equation of Continuity
Enrique Zeleny
Pitot Tube
Sara McCaslin and Fredericka Brown
Energy Balance on Pressurizing a Tank
Rachael L. Baumann
Continuous Stirred-Tank Reactor That Loses Cooling
Rachael L. Baumann
