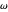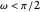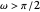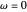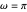Spherical Trochoid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
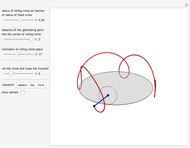
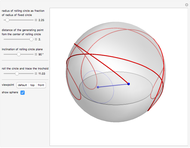
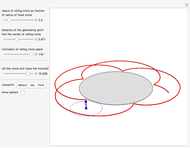
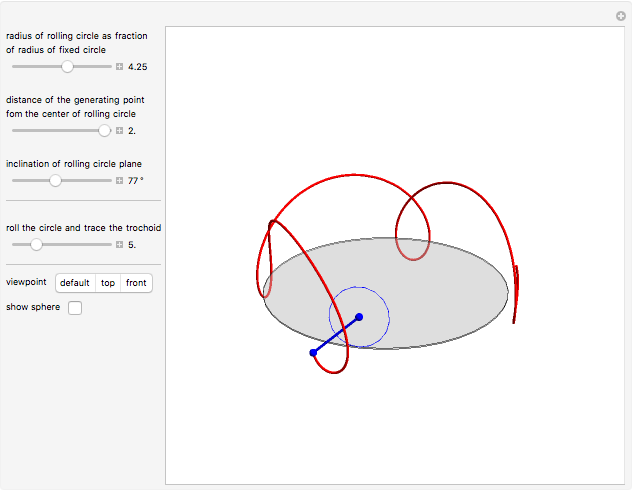
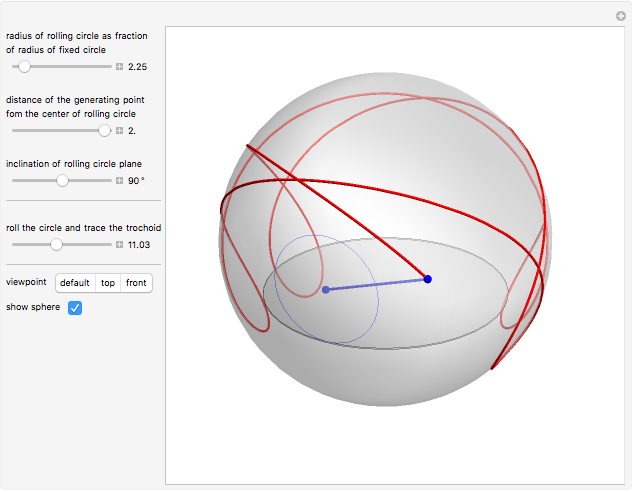
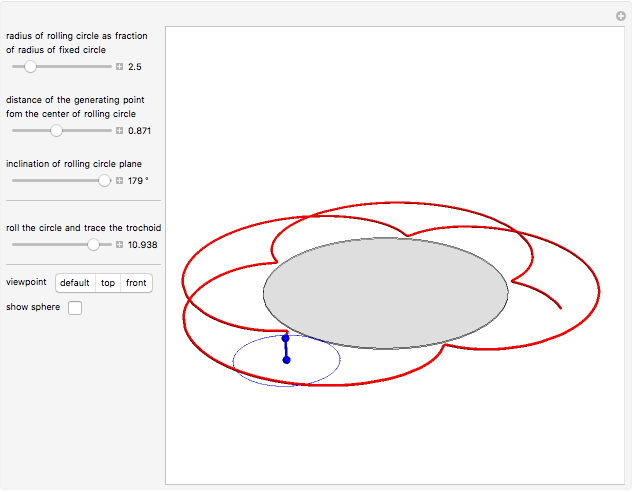
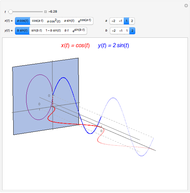
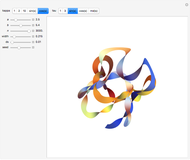
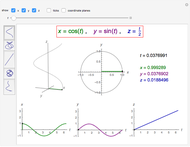
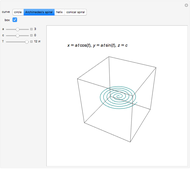
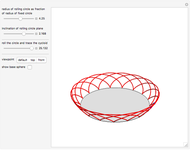
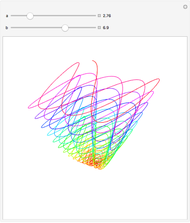
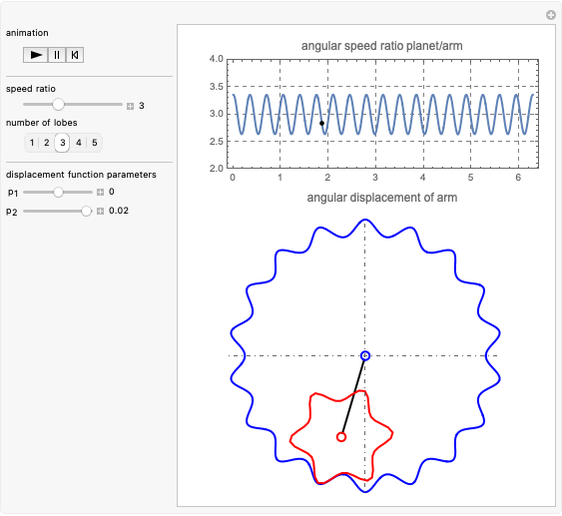
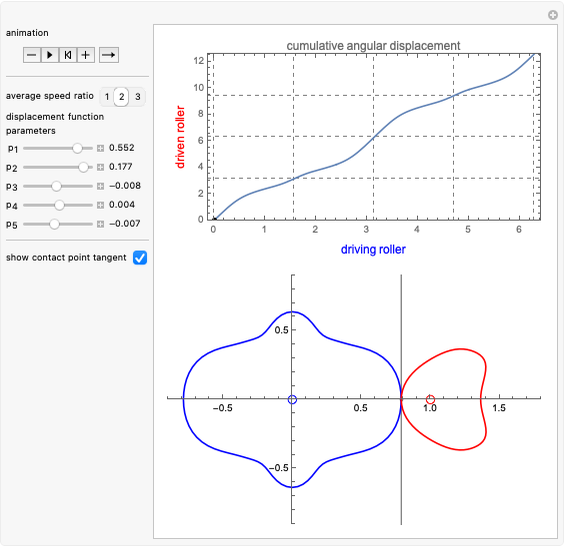
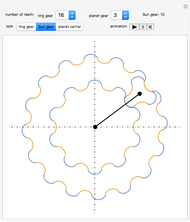
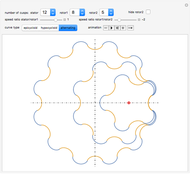
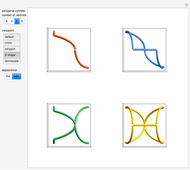
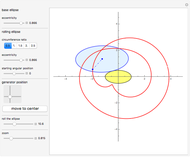
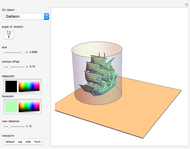
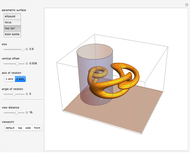
This Demonstration simulates the generation of a spherical trochoid by a point attached to a circle rolling without sliding along the edge of another circle (the base circle) on the same sphere (the base sphere).
[more]
Contributed by: Erik Mahieu (November 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let 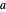 be the radius of the base circle centered at
be the radius of the base circle centered at 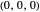 ,
,  the radius of the rolling circle and
the radius of the rolling circle and  the distance of the generating point to its center;
the distance of the generating point to its center; 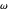 is the angle between the
is the angle between the 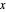 -
-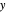 plane and the plane of the rolling circle.
plane and the plane of the rolling circle.
Let  be the angular displacement of the rolling circle along the edge of the base circle. Since the rolling circle rolls without sliding, its angular displacement around its center is
be the angular displacement of the rolling circle along the edge of the base circle. Since the rolling circle rolls without sliding, its angular displacement around its center is 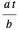 .
.
The point on a copy of the rolling circle centered at 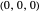 in the
in the  -
- plane and at a distance
plane and at a distance  from its center is:
from its center is:
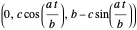 .
.
First rotate this circle by 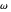 around the
around the 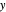 axis:
axis:
 .
.
Now translate the circle over a distance 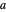 along the
along the 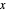 axis to get:
axis to get:
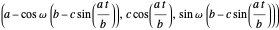 .
.
Finally, rotate this circle by an angle  around the
around the  axis:
axis:
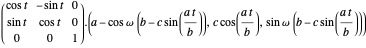 .
.
This gives the parametric equation of the spherical trochoid:
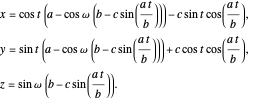
The spherical trochoid is on a sphere with center at 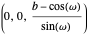 and radius
and radius 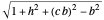 .
.
Reference
[1] H. M. Jeffery, "On Spherical Cycloidal and Trochoidal Curves," The Quarterly Journal of Pure and Applied Mathematics, 19(73), 1882 pp. 45–66. gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0019%7CLOG_0012.
Permanent Citation