Spread of a Gaussian Wave Packet with Time

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
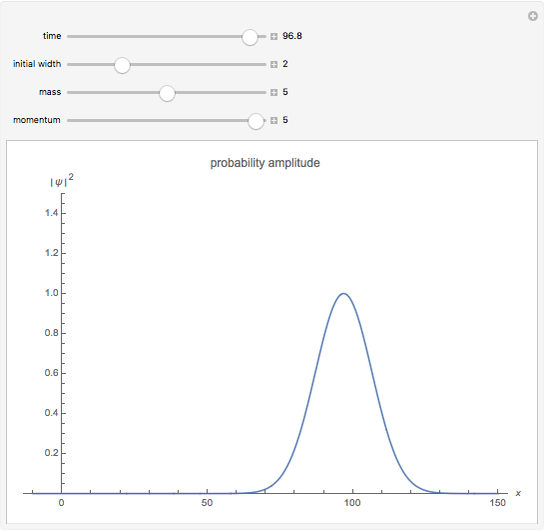
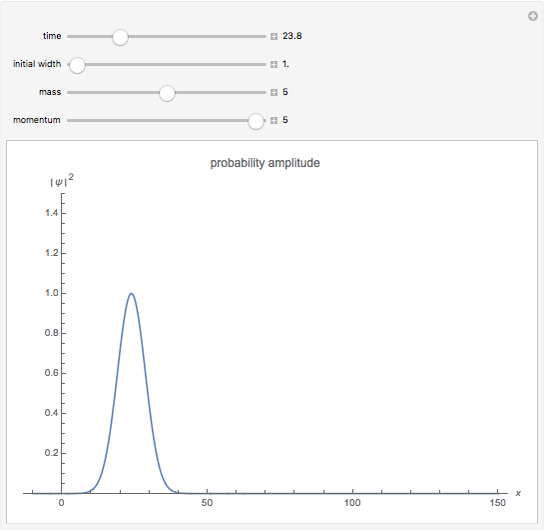
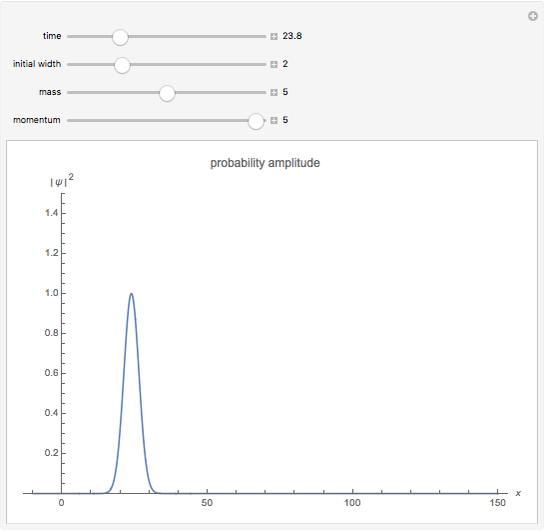
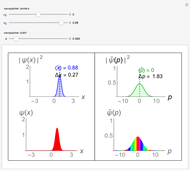
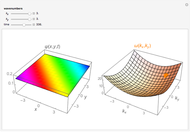
A localized free particle can be represented by a Gaussian wave packet. This Demonstration shows the spreading of a Gaussian wave packet, considering the effects of varying particle mass and momentum and initial width of the wave packet. Choose the parameters: mass, initial width and momentum, and see the evolution of the wave packet with time.
Contributed by: Radhika Prasad and Sarbani Chatterjee (June 2015)
Supervised by: S. N. Sandhya
(Miranda House, University of Delhi)
Open content licensed under CC BY-NC-SA
Details
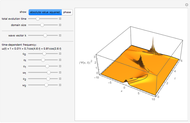
A Gaussian wave packet at time  can be represented by
can be represented by
 ,
,
where  is the initial width of the wave packet and
is the initial width of the wave packet and  is the momentum.
is the momentum.
At a later time  , the wave packet evolves with
, the wave packet evolves with
 ,
,
where  is a constant,
is a constant,  is the mass of the particle, and
is the mass of the particle, and  is a parameter that determines the corresponding width of the wave packet (
is a parameter that determines the corresponding width of the wave packet ( is the actual width). The parameter
is the actual width). The parameter  is given by
is given by
Clearly, the width increases with time  , as the wave packet spreads. For simplicity,
, as the wave packet spreads. For simplicity,  and
and  have been set equal to unity.
have been set equal to unity.
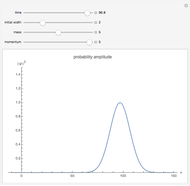
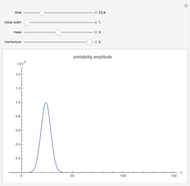
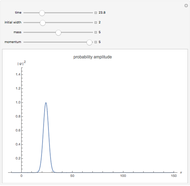
The probability amplitude is a Gaussian function centered about the point  .
.
The wave packet maintains a Gaussian shape, with changing centroid and width.
Snapshot 1: small initial width implies faster spread
Snapshot 2: initially broad wave packet spreads out more slowly
In the limiting case, of a wave packet initially equal to a Dirac delta function, it immediately transforms into an infinite plane wave.
Reference
[1] H. C. Verma, Quantum Physics, 2nd ed., Bhopura, Ghaziabad, India: Surya Publications, 2009.
Snapshots
Permanent Citation