Stability Radius for the Shortest Path Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
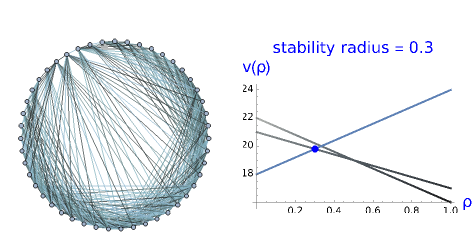
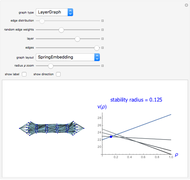
In stability theory, a quantitative characteristic called the stability radius is defined as the limit level of perturbations of problem parameters preserving optimality of a single solution (or of the solution set). These perturbations are caused by the various factors of uncertainty and randomness, such as inadequacy of mathematical models to real processes, rounding errors, calculation errors, and so on.
[more]
Contributed by: Olia Karelkina (February 2016)
Open content licensed under CC BY-NC-SA
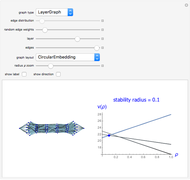
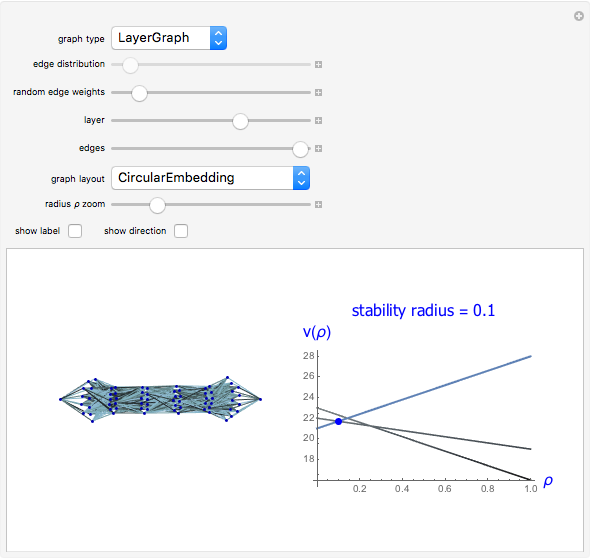
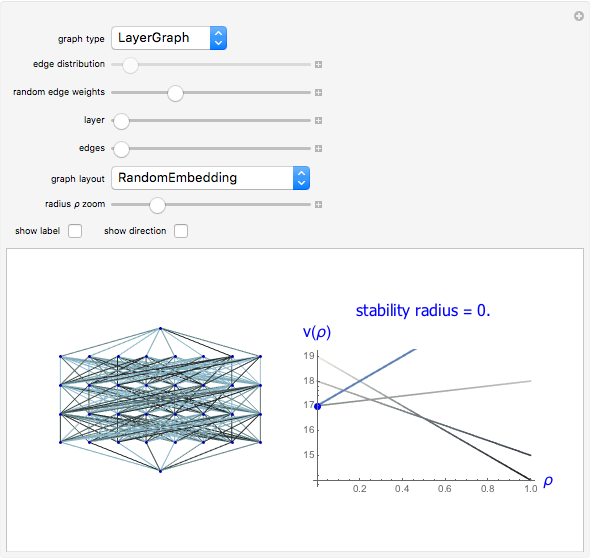
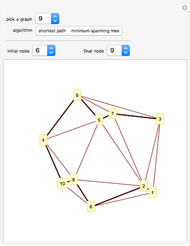
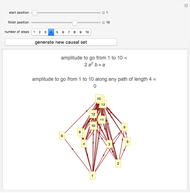
Snapshots
Details
References
[1] N. Chakravarti and A. P. M. Wagelmans, "Calculation of Stability Radii for Combinatorial Optimization Problems," Operations Research Letters, 23(1–2), 1998 pp. 1–7. doi:10.1016/S0167-6377(98)00031-5.
[2] V. Emelichev and D. Podkopaev, "Quantitative Stability Analysis for Vector Problems of 0-1 Programming," Discrete Optimization, 7(1-2), 2010 pp. 48–63. doi:10.1016/j.disopt.2010.02.001.
Permanent Citation