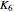Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Earth-Moon Problem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

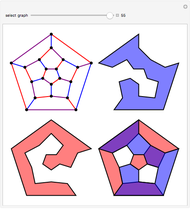
In 1959, Gerhard Ringel proposed the Earth-Moon problem. Consider a map of an alien world, in which each country is a simply connected region. Around it revolves a moon divided into colonies of the countries, each a simply connected region. Colored maps of the world and moon must use the same color for a country and its colony, and different colors for both countries that share a border on the planet and colonies that share a border on the moon. What is the minimal number of colors needed [1]?

[more]

In 1980, Thom Sulanke found a pair of planar 11-region maps that had 50 of the possible 55 borders [1]. The missing five connections make a cycle (the graph) that requires three colors in order to have no two neighboring vertices of the same color. The six countries not in the cycle are all connected, making the graph, which needs six colors. All together, nine colors are required for the Sulanke Earth-Moon map.

For this Demonstration, all 1249 maximally triangular planar graphs on 11 vertices were studied, along with their complements. A total of 790 solutions of the type were identified.

[less]

Contributed by: Ed Pegg Jr (September 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

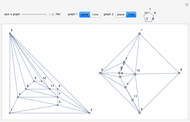
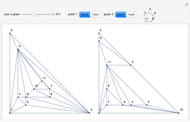
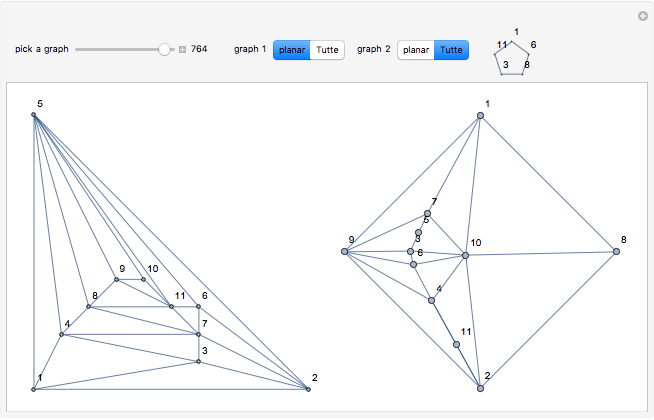
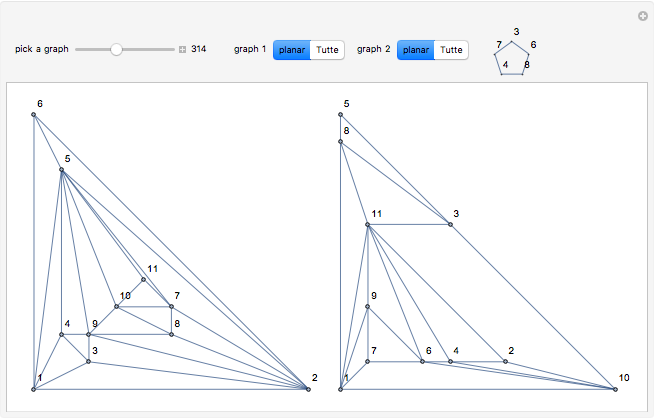
A related unsolved problem involves the geometric thickness of a graph. With all edges being straight lines, what is the minimal number of colors needed so that no two edges of the same color cross? The Paley-13 graph has geometric thickness 2, as shown below.

Using rectangle visibility graphs, geometric thickness-2 graphs with vertices and edges are known. The proven maximum for vertices is edges, but no examples are known. The graphs in this Demonstration use 11 vertices and 50 edges. If a combined form can have two edges removed so that no two edges of the same color cross, then that would provide a solution.

References

[1] N. Hartsfield and G. Ringel, Pearls in Graph Theory, Mineola, NY: Dover Books, 2003, p. 204.

[2] D. Eppstein. "The Geometry Junkyard: Layered Graph Drawing." (Sep 22, 2015) www.ics.uci.edu/~eppstein/junkyard/thickness.

[3] B. Jackson, "Variations on Ringel's Earth–Moon Problem," Discrete Mathematics, 211(1–3), 2000 pp. 233–242. doi:10.1016/S0012-365X(99)00278-2.

[4] J. Battle, F. Harary, and Y. Kodama, "Every Planar Graph with Nine Points Has a Non-planar Complement," Bulletin of the American Mathematical Society, 68, 1962 pp. 569–571. www.ams.org/journals/bull/1962-68-06/S0002-9904-1962-10850-7/S0002-9904-1962-10850-7.pdf.

[5] E. Mäkinen and T. Poranen. "An Annotated Bibliography on the Thickness, Outerthickness, and Arboricity of a Graph." (Sep 22, 2015) www.sis.uta.fi/~tp54752/pub/thickness-bibliography/thickness-bibliography.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send