Stackelberg Equilibrium Set in 2x2 Mixed Extended Games

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
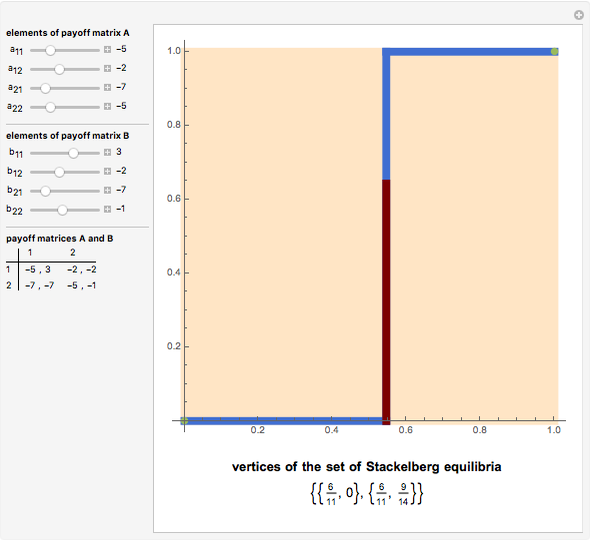
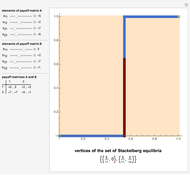
Consider a bimatrix ( ) mixed extended Stackelberg game. Player 1 has the payoff matrix
) mixed extended Stackelberg game. Player 1 has the payoff matrix  . Player 2 has the payoff matrix
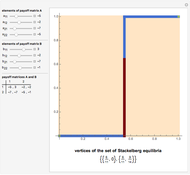
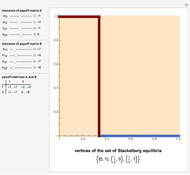
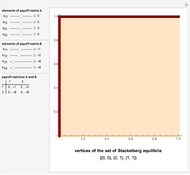
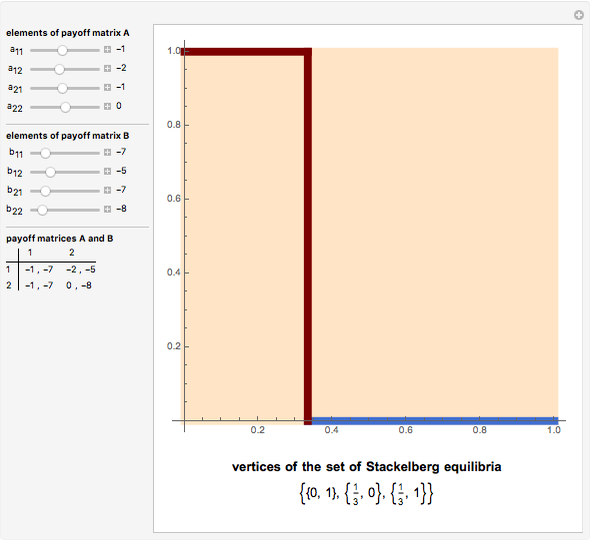
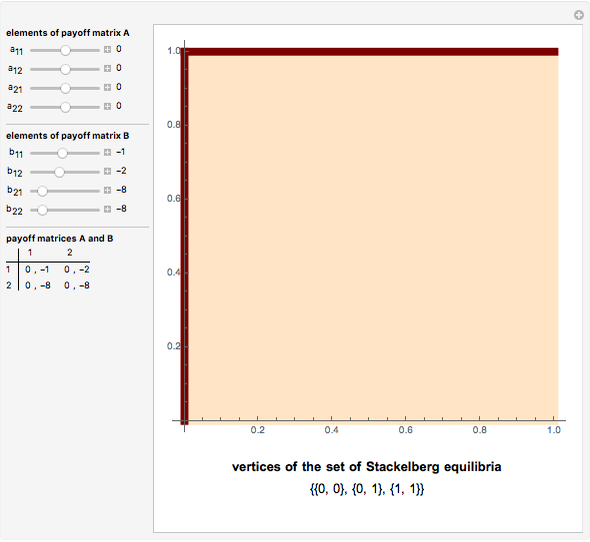
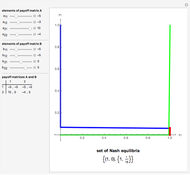
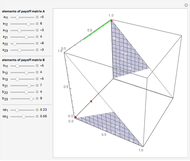
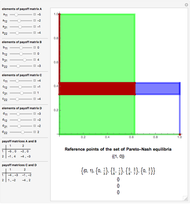
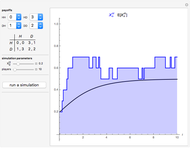
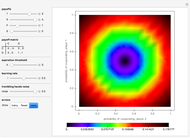
. Player 2 has the payoff matrix  . Player 1 is the leader and he moves first. Player 2 is the follower and he moves second. The leader knows ex ante (beforehand) that the follower observes his action. The set of Stackelberg equilibria (red) in a particular game is determined as the solution-of-optimization problem on the graph-of-best-response mapping (blue) of the player 2 (follower); its vertices are given at the bottom. Green points are not equilibrium, but have the same value of the cost function of the leader on the interior vertex of the set of Stackelberg equilibria.
. Player 1 is the leader and he moves first. Player 2 is the follower and he moves second. The leader knows ex ante (beforehand) that the follower observes his action. The set of Stackelberg equilibria (red) in a particular game is determined as the solution-of-optimization problem on the graph-of-best-response mapping (blue) of the player 2 (follower); its vertices are given at the bottom. Green points are not equilibrium, but have the same value of the cost function of the leader on the interior vertex of the set of Stackelberg equilibria.
Contributed by: Valeriu Ungureanu and Victoria Lozan (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Sliders define the elements of the  matrix. First, mixed strategies of both the players
matrix. First, mixed strategies of both the players  and
and  ) are used for the graphic representation of the set of Stackelberg equilibria. The values of the second strategy of the players are simply
) are used for the graphic representation of the set of Stackelberg equilibria. The values of the second strategy of the players are simply 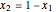 and
and  .
.
Reference:
H. von Stackelberg, Marktform und Gleichgewicht (Market Structure and Equilibrium), Wien/Berlin: Springer, 1934.
Permanent Citation