Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

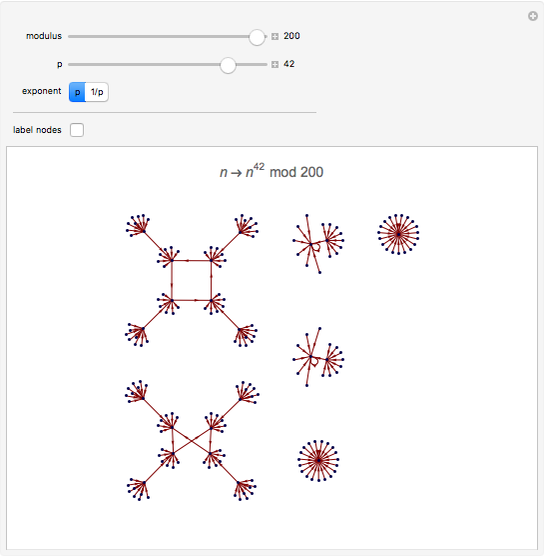
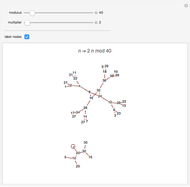
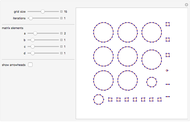
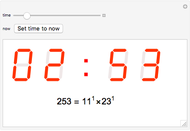
State Transition Diagrams for Modular Powers

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

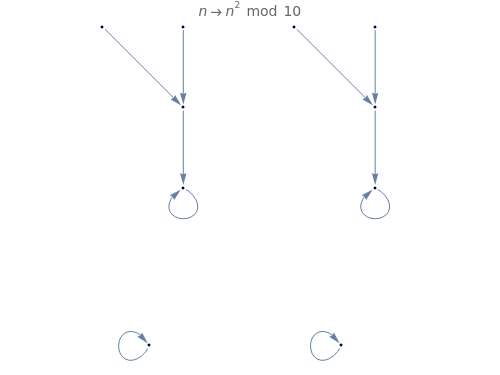
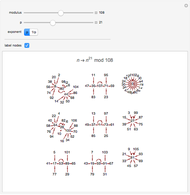
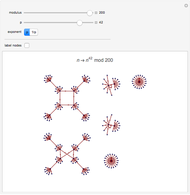
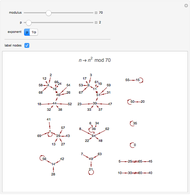
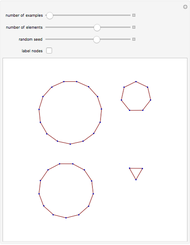
Each point represents an integer, joined to the point representing the result of the modular power. The structure of the final "state transition diagram" varies greatly with both the multiplier and modulus.

Contributed by: Stephen Wolfram (March 2011)
Based on a suggestion by: Stan Wagon
With additional contributions by Robert Baillie
Open content licensed under CC BY-NC-SA

Snapshots

Details

Mouse over points to see the integers to which they correspond. A number pointing to means the number has no root for the given .

Fermat's little theorem, Euler's theorem, quadratic residues and nonresidues, and other number theoretic phenomena are visible.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send