Steinhart-Hart Approximations for Thermistor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
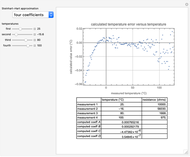
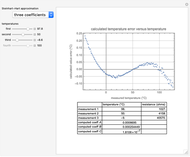
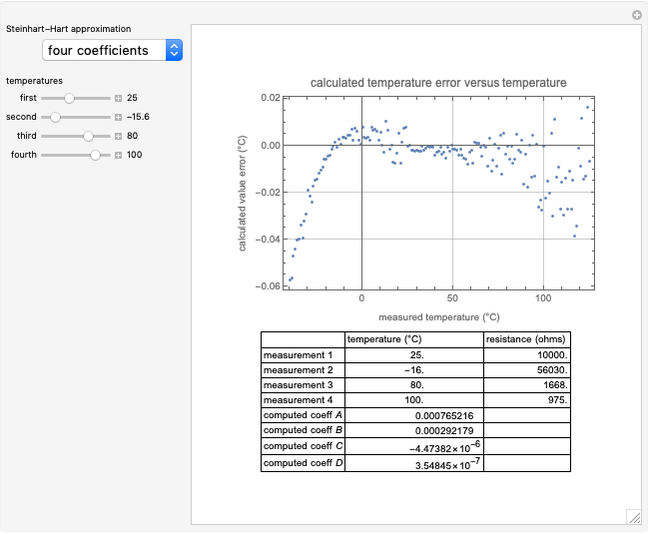
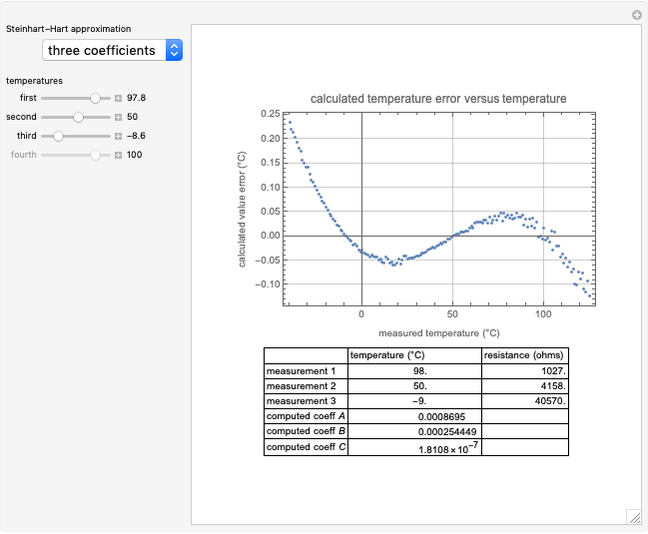
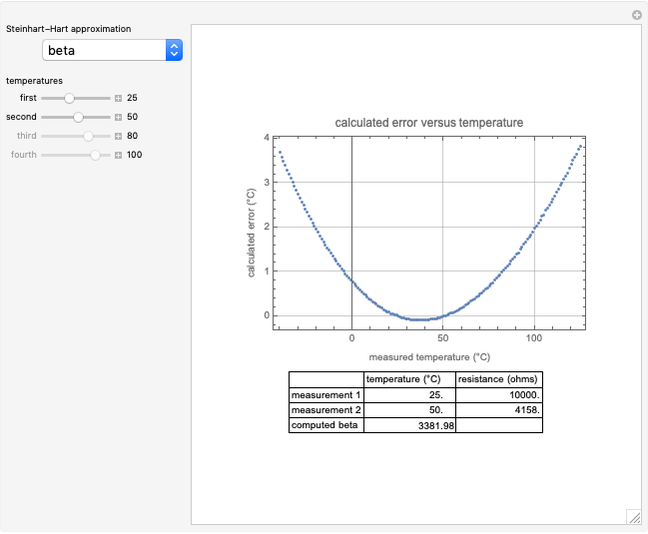
This Demonstration considers a full set of measurements of a negative temperature coefficient thermistor and lets you select the approximation method and the data points to be used for a corresponding version of the Steinhart–Hart approximation. The computed Steinhart–Hart coefficients are displayed along with a plot of the difference between the measured and approximated values (the temperature error).
Contributed by: Kirby Goulet (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Specification of a negative temperature coefficient thermistor is commonly expressed in terms of the coefficients in a Steinhart–Hart approximation. There are three common sets of coefficients: the beta coefficient that is computed from two measurement data points at two specified temperatures, the three-coefficient approximation that requires three measured data points and the four-coefficient approximation that requires four data points for curve fitting.
Two coefficients (beta constant):
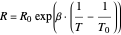
Three coefficients (Steinhart–Hart equation):
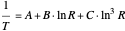
Four coefficients (Steinhart–Hart equation):
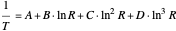
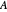 ,
, 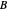 ,
, 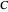 and
and  are Steinhart–Hart coefficients and
are Steinhart–Hart coefficients and  is a constant commonly specified for thermistors. The coefficients for fitting the four-coefficient equation are not necessarily the same as those for fitting the three-coefficient equation.
is a constant commonly specified for thermistors. The coefficients for fitting the four-coefficient equation are not necessarily the same as those for fitting the three-coefficient equation.
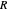 is the thermistor resistance in ohms at temperature
is the thermistor resistance in ohms at temperature 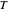 .
.
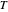 is the thermistor temperature in degrees Kelvin.
is the thermistor temperature in degrees Kelvin.
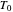 is a reference temperature used for one of the measured data points used to calculate the
is a reference temperature used for one of the measured data points used to calculate the  constant. Commonly, this is 25 °C.
constant. Commonly, this is 25 °C.
 is the thermistor resistance at the reference temperature
is the thermistor resistance at the reference temperature 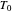 .
.
The measured data [1] is taken from the manufacturer's data for the model TDK part number NTCG063JF103FTDS.
Reference
[1] "NTCG063JF103FTDS." TDK Product Center. (Aug 6, 2021) product.tdk.com/en/search/sensor/ntc/chip-ntc-thermistor/info?part_no=NTCG063JF103FTDS.
Permanent Citation