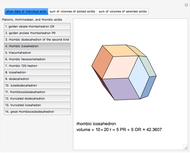
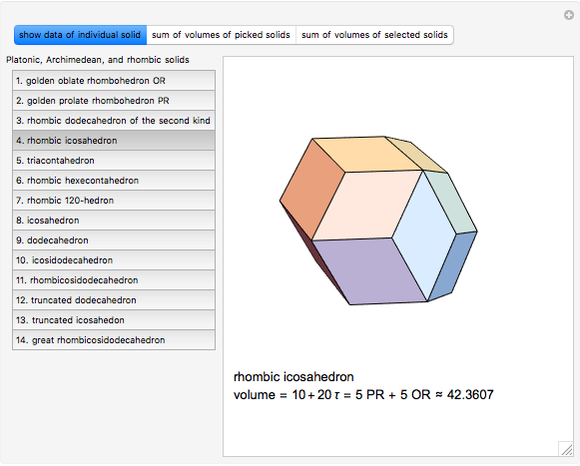
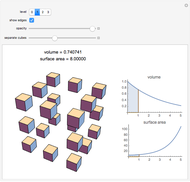
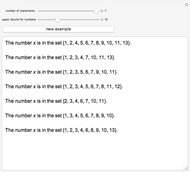
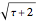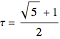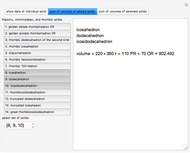
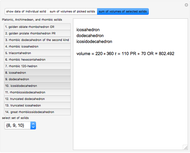
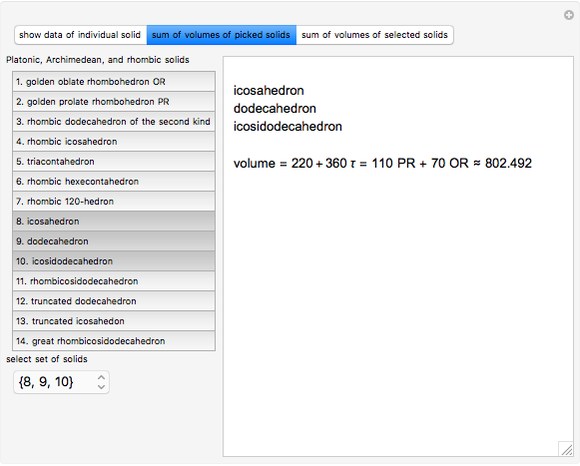
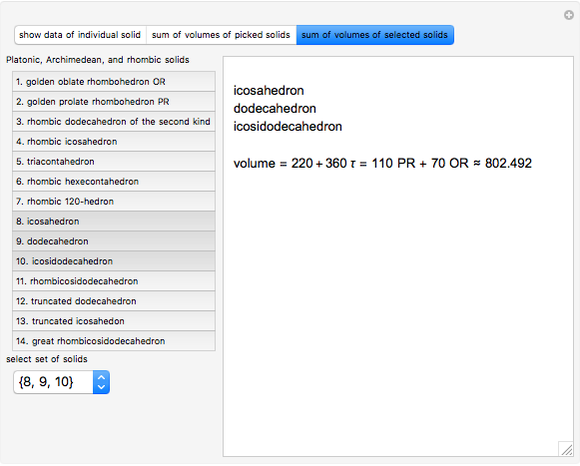
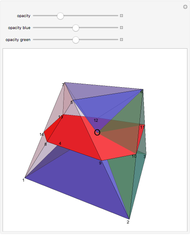
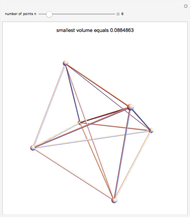
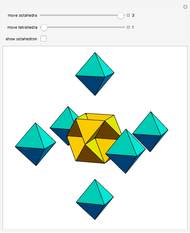
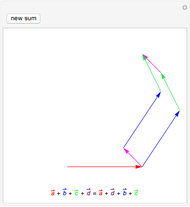
This Demonstration calculates the exact volumes of some rhombic, Platonic, and Archimedean solids using the exact coordinates of these solids. The length of an edge of a rhombic solid is , where is the golden ratio. The edge length of the other solids is 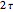. The volumes of some combinations (disjoint unions), for instance of the icosahedron, the dodecahedron, and the icosidodecahedron, are an integral linear combination of the volumes of the prolate golden rhombohedron (PR) and of the oblate golden rhombohedron. This does not mean that such a combination can be dissected into a cube, but the combination of the icosahedron, the dodecahedron, and the icosidodecahedron has a Dehn invariant 0, so by Sydler's theorem it is possible to dissect the combination to form a cube [1]. In fact this set of solids is equidecomposable with the set consisting of the triacontahedron, the hexecontahedron, and 120-hedron. Select these sets and verify that the corresponding volumes are equal.