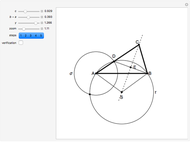
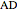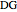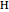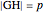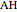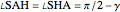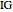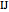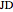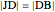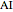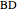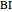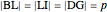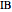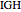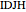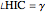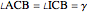17b. Construct a Triangle Given the Length of an Angle Bisector, the Angle at Another Vertex and the Distance from the Third Vertex to the Angle Bisector

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
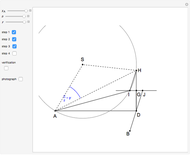
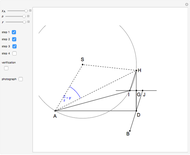
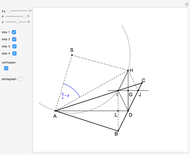
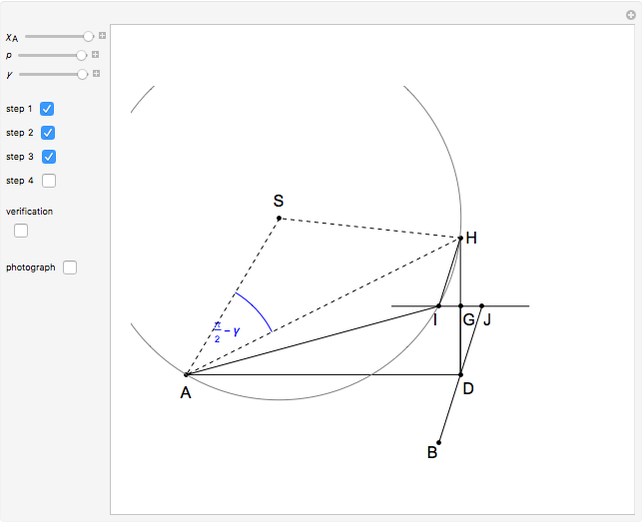
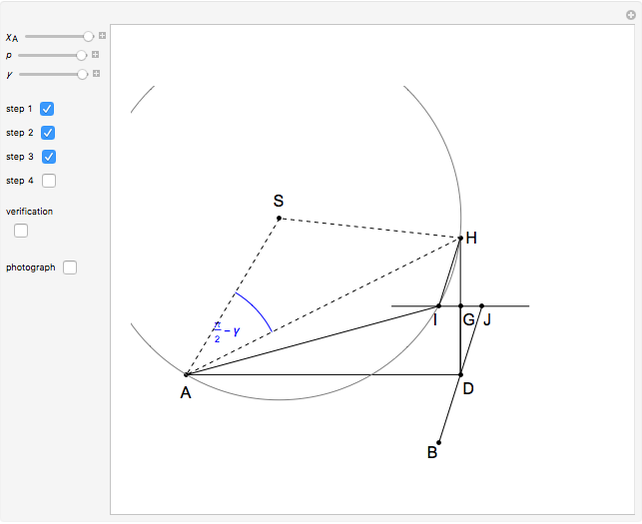
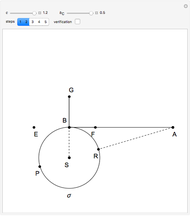
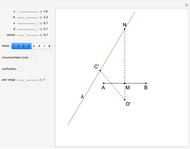
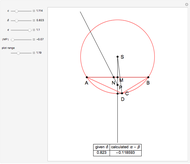
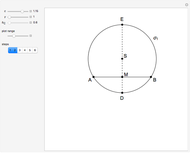
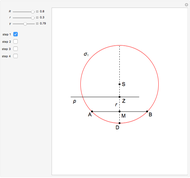
This Demonstration shows an alternative construction of a triangle 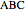 given the angle
given the angle  at
at  , the length
, the length 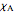 of the angle bisector at
of the angle bisector at 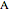 and the length
and the length 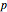 of the perpendicular from
of the perpendicular from 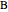 to the bisector.
to the bisector.
Contributed by: Nada Razpet, Marko Razpet and Izidor Hafner (August 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
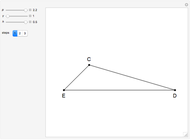
The problem appeared in Wiegand's book [4, p. 147]; the photograph is from that book. One solution is also given in [5, p.156].
When professor Plemelj was in Chernivtsi (1908–1914, then in the Austrian–Hungarian Empire, now in Ukraine), he talked with two students about the construction problem in a certain textbook that he had been given by his teacher Borstner when attending gymnasium. They brought him a copy of the book, but Plemelj forgot for the second time to write down the title, so we still do not know its title.
He looked for the book in Ljubljana after the First World War but could not find it, but he found the problem of this Demonstration in [4].
Using the construction from [4], Plemelj found a nice solution of his original problem (given base  , the altitude
, the altitude  and the difference
and the difference  of the angles at base).
of the angles at base).
This Demonstation does the opposite. Using the construction from Borstner’s book, we solve the problem in Wiegand’s book. An almost identical approach is given in [5, p. 93].
References
[1] Wikipedia. "Josip Plemelj." (Aug 23, 2017) en.wikipedia.org/wiki/Josip_Plemelj.
[2] J. J. O'Connor and E. F. Robertson. "Josip Plemelj." MacTutor. (Aug 23, 2017) www-history.mcs.st-andrews.ac.uk/Biographies/Plemelj.html.
[3] J. Plemelj, Iz mojega življenja in dela (From My Life and Work), Obzornik mat. fiz., 39, 1992 pp. 188–192.
[4] M. Bland and A. Wiegand, Geometrische Aufgaben für Hohëre Lehranstalten, Braunschweig: Schewetschke und Sohn, 1865.
[5] D.S. Modic, Trikotniki, Konstrukcije, Algebrske Rešitve, Ljubljana: Math d.o.o., 2009.
Permanent Citation