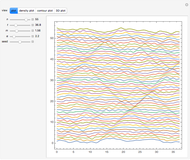
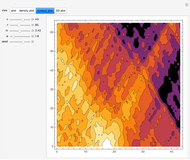
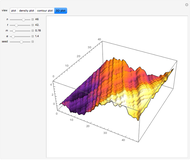
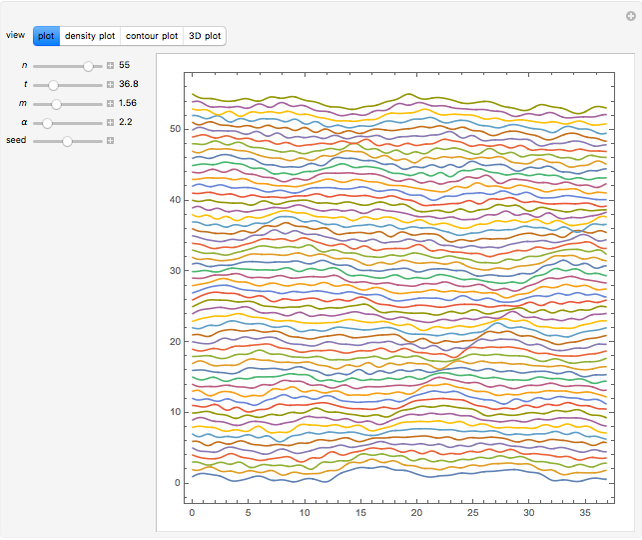
The Fermi–Pasta–Ulam problem is named after the pioneering numerical experiments realized by Enrico Fermi, John Pasta, and Stanislaw Ulam in 1955 using the Los Alamos MANIAC computer. Based on the Debye theory of crystals, they considered a system of particles of mass connected by harmonic springs, but introduced a quadratic nonlinear term. They expected ergodic behavior, but to their surprise, observed recurrent behavior. The continuum limit of the model is the Korteweg–de Vries nonlinear partial differential equation.