The Gambler's Ruin
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
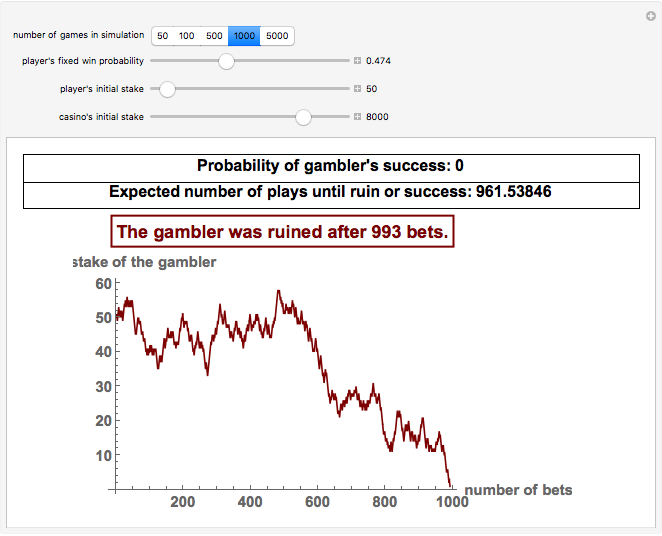
The gambler starts with an 
unit stake and the casino or house starts with 
units. They repeatedly play a game for which the gambler has a fixed probability 
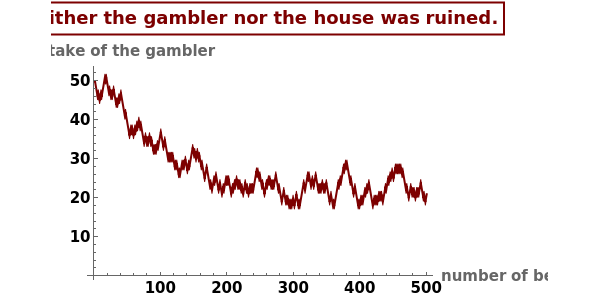
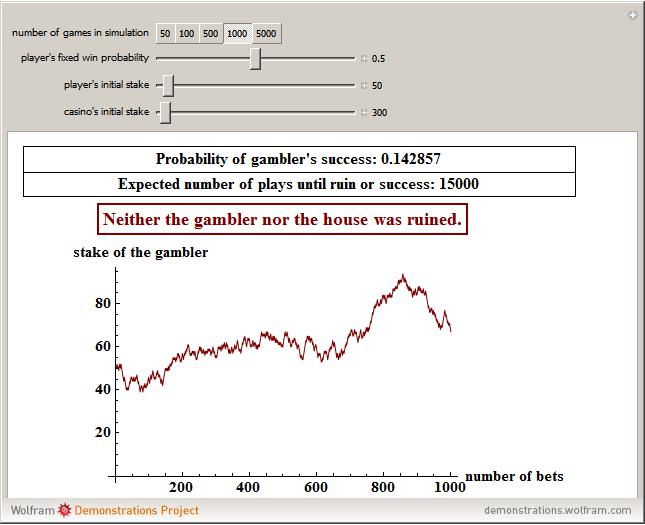
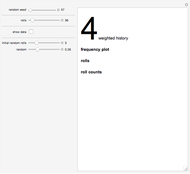
of winning and the winner gets 1 unit from the loser. Play continues until the gambler "succeeds" by acquiring 
units or is "ruined" by dropping to 0 units. This Demonstration computes the probability that the gambler will succeed by breaking the bank. Subtracting this probability from 1 gives the gambler's ruin probability. The theoretical expected number of plays of the game until success or ruin is also computed and a simulation gives empirical results for the various parameter values. In the example shown in the thumbnail we use 
, the player's probability of winning an "even money" bet in American roulette.
Contributed by: Ed Packel (Lake Forest College) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
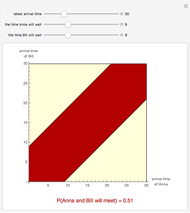
Snapshot 1: a fair game—in such cases the gambler's overall success probability is simply 
, the gambler's proportion of the total stake and the expected number of plays until ruin is 
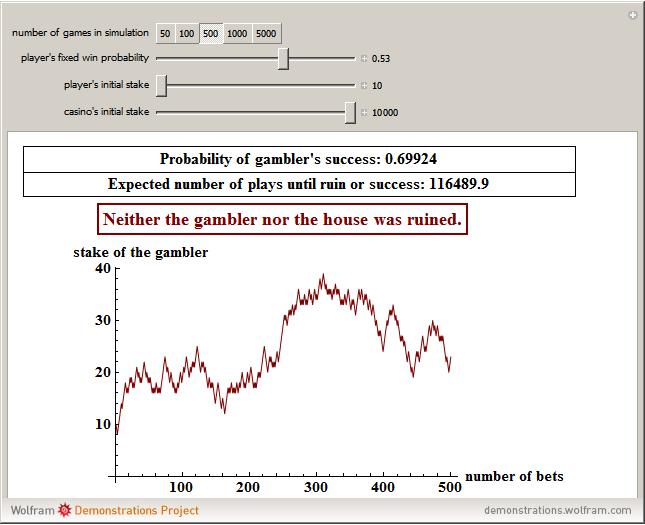
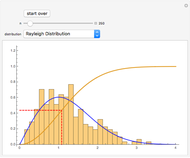
Snapshot 2: 
, which is about what an expert card counter in blackjack might achieve; in the simulation, the gambler generates a nice profit, but would require a very long time to break the bank
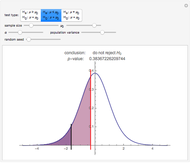
Snapshot 3: results also apply to two individuals playing "head on"; here the "player" triumphs with the help of a larger bankroll, despite the fact that the odds slightly favor the opponent
Related results: Derivation of the relevant formulas for probability of success and for expected time for success or ruin involves a nice application of recurrence relations. It also provides an interesting example of an absorbing Markov chain. For a more elementary approach, see Chapter 6 of the reference below.
E. Packel, The Mathematics of Games and Gambling, 2nd ed., Washington: The Mathematical Association of America, 2006.
Permanent Citation
The Three-Tower Problem
Heikki Ruskeepää
A Reluctant Random Walk
Heikki Ruskeepää
Rolling Two Dice with Weighted History
Laura Shou
Walking Randomly Until No Shoes Are Available
Heikki Ruskeepää
A Random Meeting
Heikki Ruskeepää
The Method of Inverse Transforms
Ryan Carroll, Adam Joplin, Jeff Hamrick, and Eric Stradley
Records in Sequences of Random Variables
Heikki Ruskeepää
Hypothesis Tests about a Population Mean
Chris Boucher
The Birthday Problem
Chris Boucher
Finite-State, Discrete-Time Markov Chains
Chris Boucher
