Rearranging the Alternating Harmonic Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
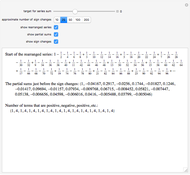
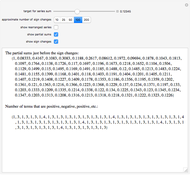
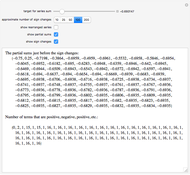
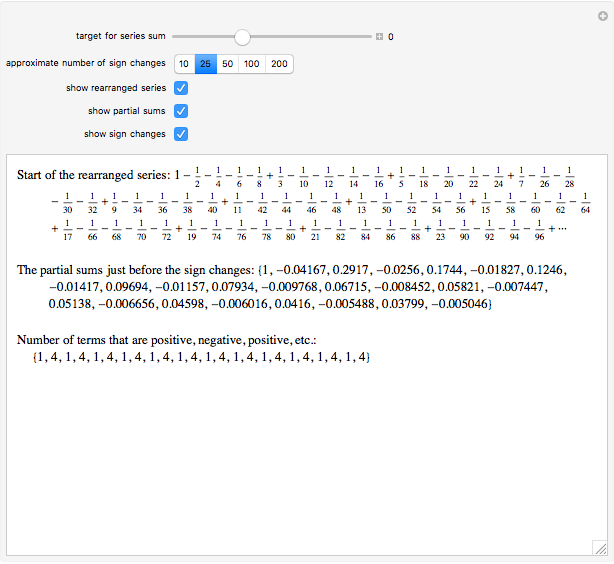
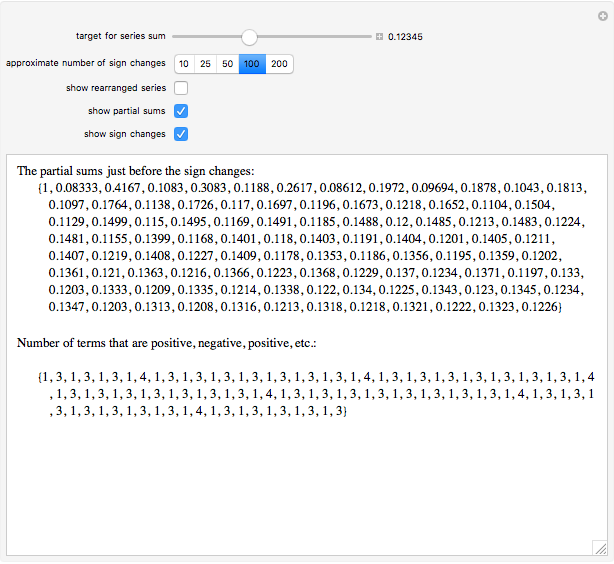
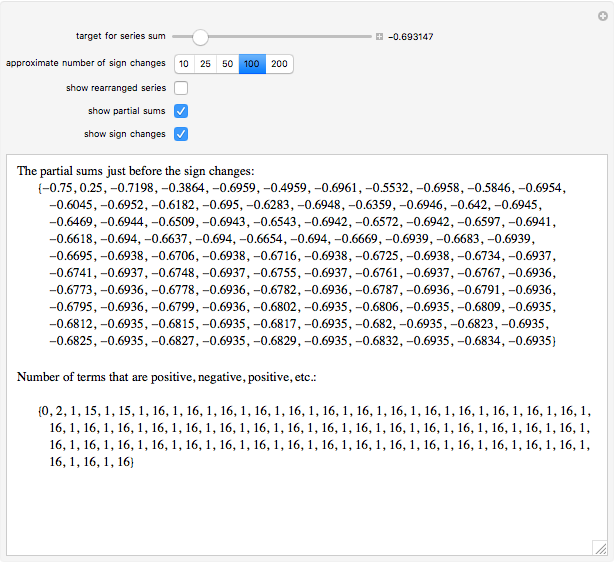
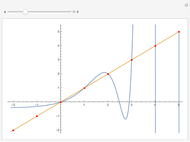
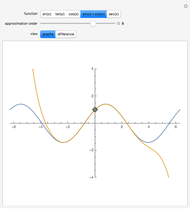
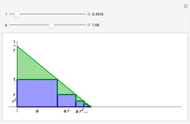
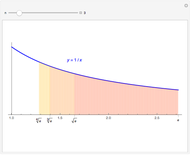
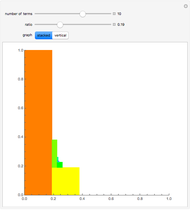
Terms in the alternating harmonic series (or any other conditionally convergent series) can be rearranged to achieve any desired real number as the sum. This Demonstration allows you to control the target sum and various options to see (part of) the rearranged series, the partial sums, and the pattern of sign changes. By default, the target is set to 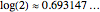 .
.
Contributed by: Ed Packel (Lake Forest College) and Stan Wagon (Macalester College) (December 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
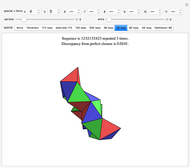
Snapshot 1: making the alternating harmonic series disappear: rearranging terms to achieve a sum of zero leads to a simple and not very well-known identity for 0
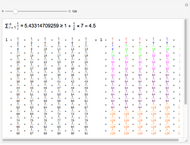
Snapshot 2: convergence to 0.12345
Snapshot 3: going negative: the rearranged series will start with negative terms
Related results:
It turns out that a limiting ratio  of positive to negative terms in the partial sums will result in a sum
of positive to negative terms in the partial sums will result in a sum  .
.
Conversely, to achieve a sum  , the desired ratio should approach
, the desired ratio should approach  .
.
For details, see these references:
E. Packel and S. Wagon, "Rearrangement Patterns for the Alternating Harmonic Series," Mathematica in Education, 3(2), 1994 pp. 5–10.
C. C. Cowen, K. R. Davidson, and R. P. Kaufman, "Rearranging the Alternating Harmonic Series," American Mathematical Monthly, 87, 1980 pp. 817–819.
Permanent Citation