Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Parametrized Szilassi Polyhedron

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

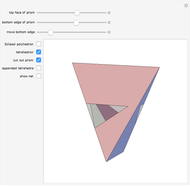
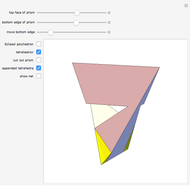
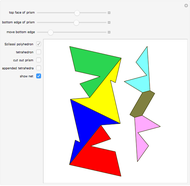
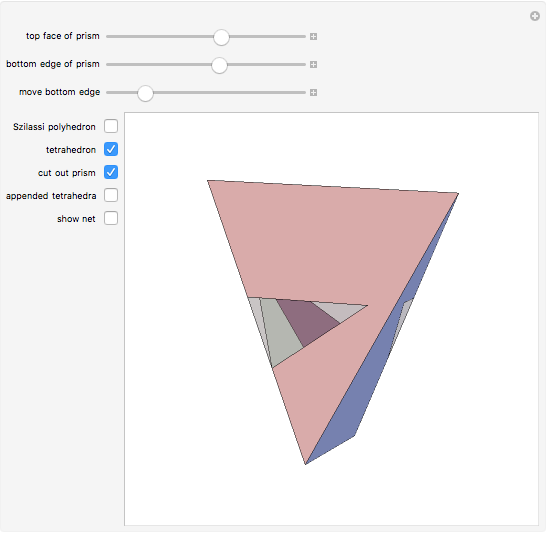
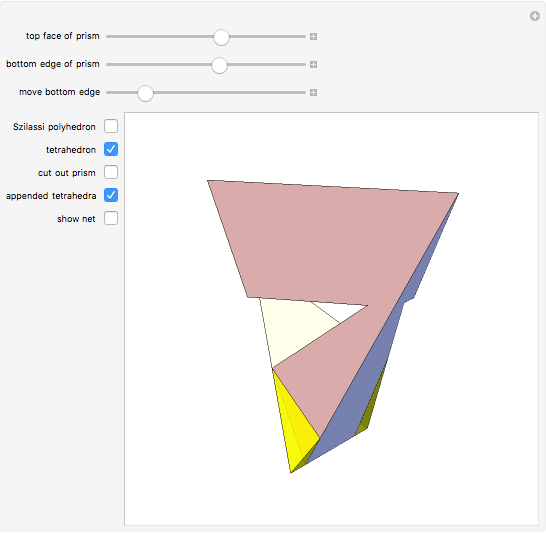
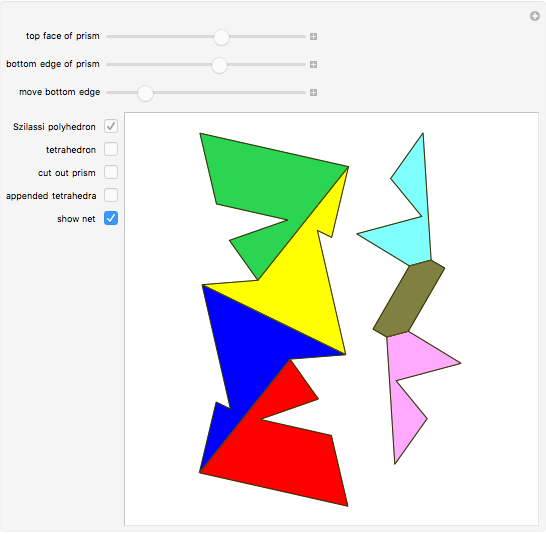
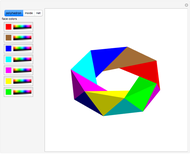
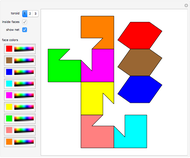
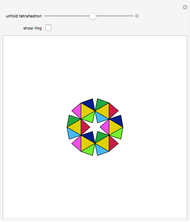
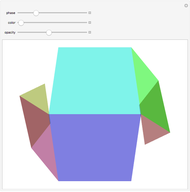
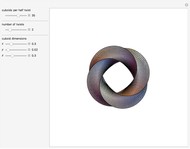
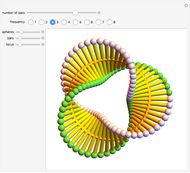
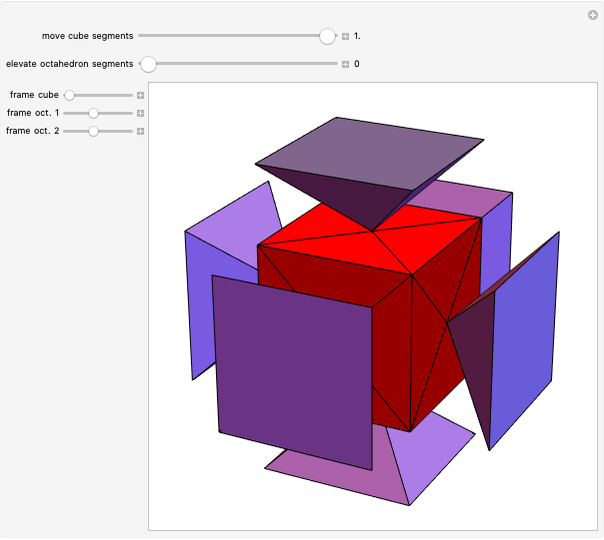
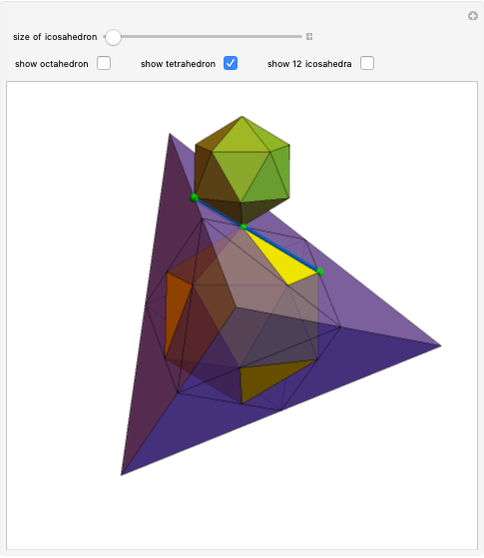
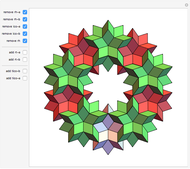
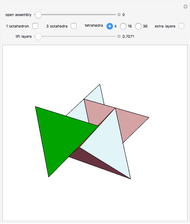
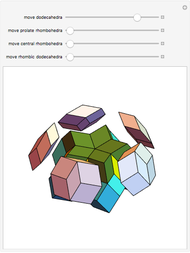
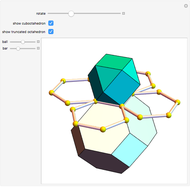
The following steps construct a regular toroid with seven faces, the Szilassi polyhedron.

[more]

1. Take a tetrahedron with isosceles triangles as faces.

2. Drill the tetrahedron with a three-sided prism, one of whose faces is parallel to the base of the isosceles triangles; the prism's opposing faces intersect two opposing edges of the tetrahedron. This gives a seven-faced polyhedron that has five hexagonal faces and two quadrilateral faces. (The top face and the bottom edges of the prism can be selected arbitrarily.)

3. Supplement the polyhedron with two small tetrahedra, whose faces are aligned in the planes of the existing faces. Move the lower edge of the prism bisecting the edges of the triangle closer to the opposite face, so that the two quadrilaterals in step 2 are extended to hexagons, parallel to the plane of the exterior face of the added tetrahedra.

4. This gives a polyhedron with seven faces. Any two faces of this polyhedron have a polygon edge in common.

In 1977, a different procedure led to the discovery of this polyhedron.

[less]

Contributed by: Lajos Szilassi (University of Szeged, Hungary) and Sándor Kabai (May 2008)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The Szilassi polyhedron is a polyhedral realization of a regular map (namely, the Heawood map).

Recall the classical definition [1]:

"A map is said to be regular if its automorphism group contains two particular automorphisms: one, say , which cyclically permutes the edges that are successive sides of one face, and another, say , which cyclically permutes the successive edges meeting at one vertex of this face."

Reference

[1] H. S. M. Coxeter and W. O. Moser, Generators and Relations for Discrete Groups, Berlin: Springer-Verlag, 1972 pp. 101–102.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send