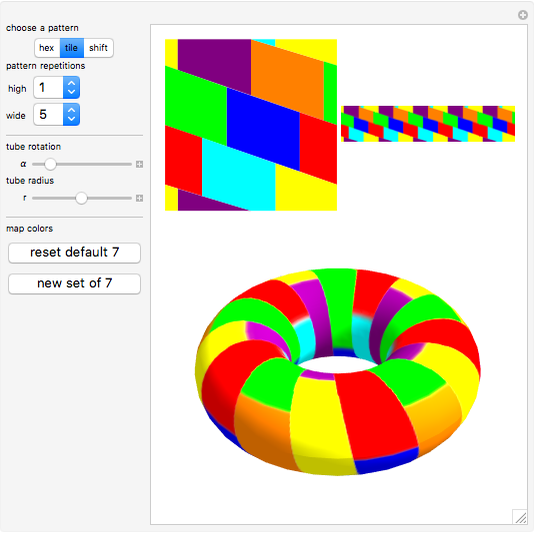
Map Coloring on a Torus

Initializing live version

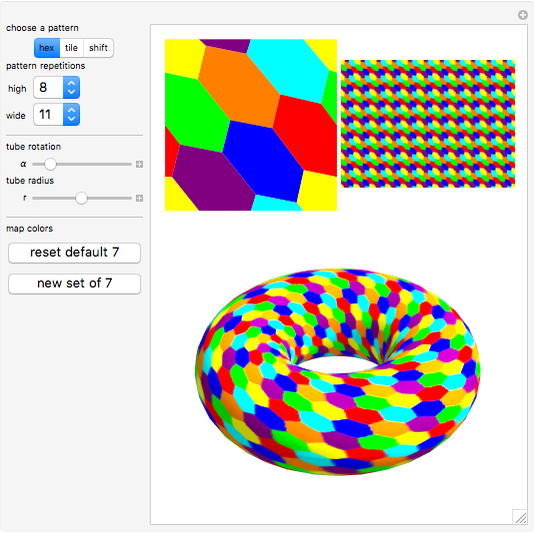
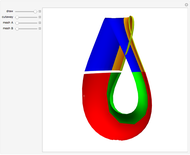
Heawood proved that seven colors are sufficient to color a map on the surface of a torus so that no two bordering areas share the same color.

Contributed by: Erik Mahieu (July 2012)
Open content licensed under CC BY-NC-SA

Snapshots

The hex pattern used in this Demonstration was adapted from [1].

The tile pattern used is based on [2].

For an extensive study about map coloring on a torus, see [3].

For a different pattern used for seven-coloring a torus, see [4].

References

[1] Wikipedia. "Heawood Conjecture." (Jul 17, 2012) en.wikipedia.org/wiki/Heawood_conjecture.

[3] John Leech, "Seven Region Maps on a Torus," The Mathematical Gazette, 39(328), 1955 pp. 102–105. www.jstor.org/stable/3609970.

[4] Izidor Hafner. "Seven-Coloring of a Torus" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/SevenColoringOfATorus.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send