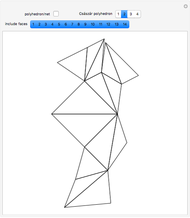
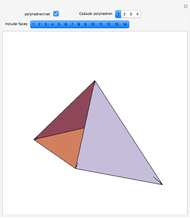
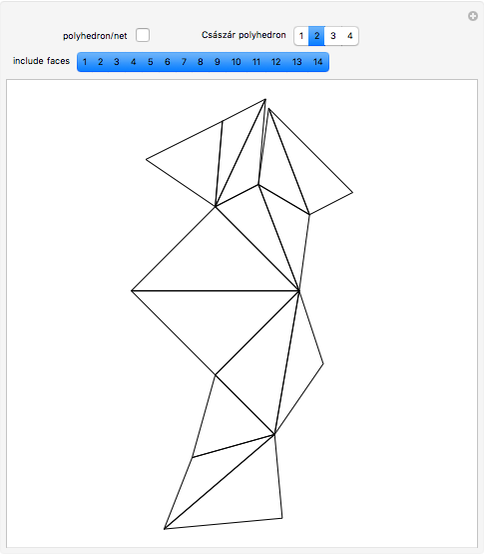
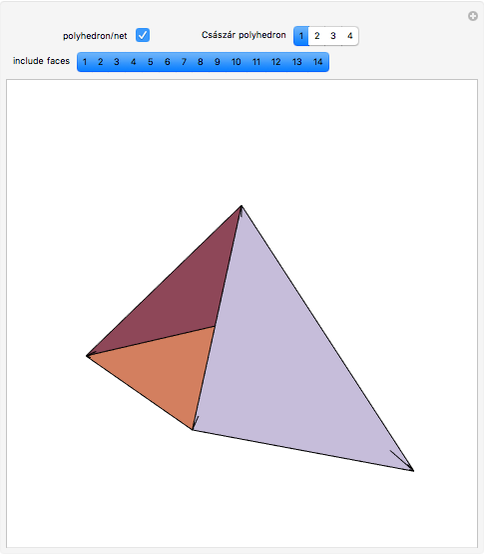
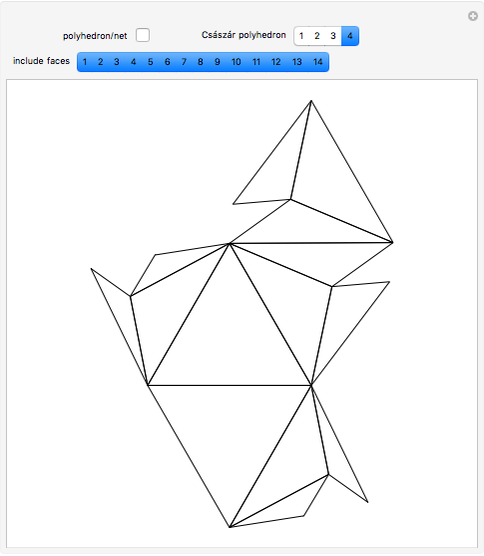
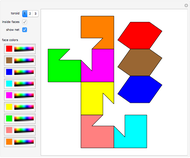
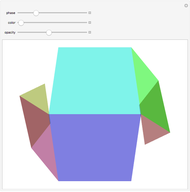
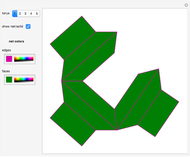
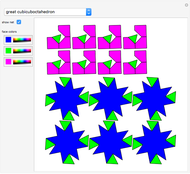
A Császár polyhedron is a nonconvex polyhedron, topologically equivalent to a toroid, with 14 triangular faces. This polyhedron has no diagonals, every pair of vertices being connected by an edge (in common with the tetrahedron). The Császár polyhedron has four visibly different versions. This Demonstration illustrates each version and its net.