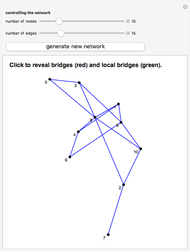
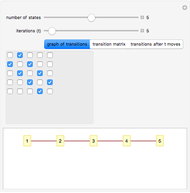
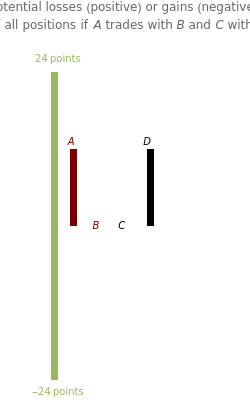The Power-Dependence Solution to Five Exchange Networks

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
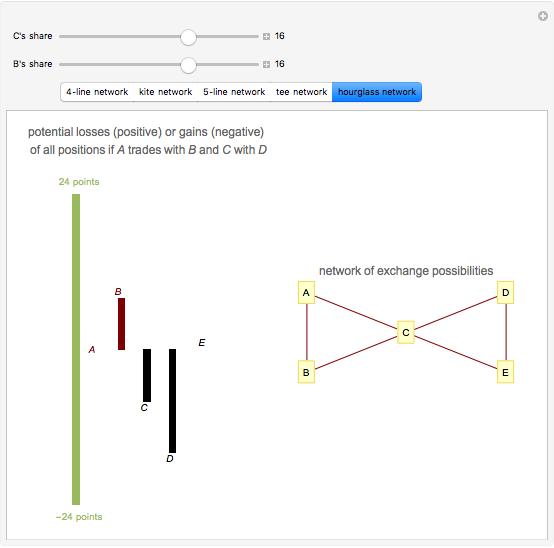
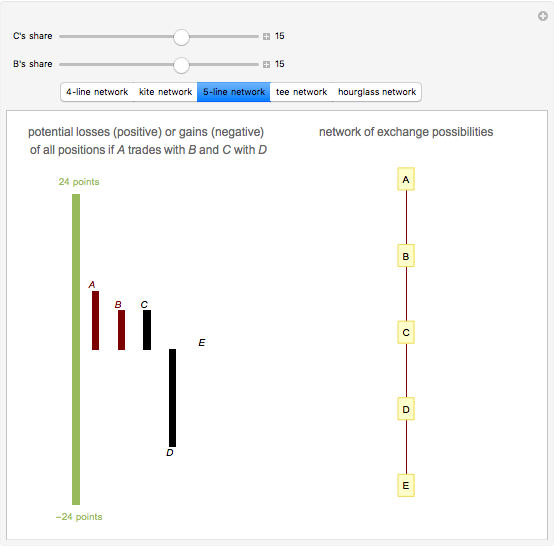
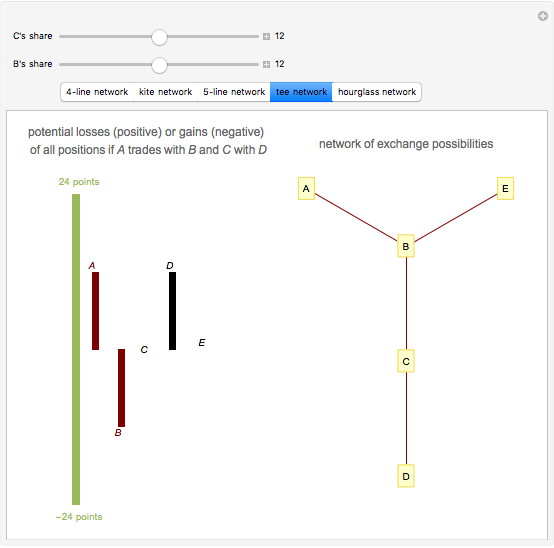
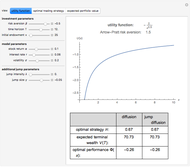
The power-dependence solution to exchange networks assumes that both members of every exchange have equally good alternatives outside the exchange; this solution is an application of the game-theoretic concept of the kernel [2] to exchange networks. All the illustrated networks have four or five nodes and all exchanges are worth 24 points. In every network, nodes 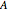 and
and 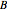 divide 24 points, as do nodes
divide 24 points, as do nodes 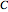 and
and  . You can try to equalize dependence within exchanging pairs by controlling the amounts earned by nodes
. You can try to equalize dependence within exchanging pairs by controlling the amounts earned by nodes 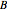 and
and 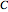 .
.
Contributed by: Phillip Bonacich (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
[1] K. S. Cook and T. Tamagishi, "Power in Exchange Networks: A Power-Dependence Formulation," Social Networks, 14(3-4), 1992 pp. 245–265.
[2] R. B. Myerson, Game Theory: Analysis of Conflict, Cambridge: Harvard University Press, 1991 p. 454.
Permanent Citation