The Riemann Zeta Function in Four Dimensions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
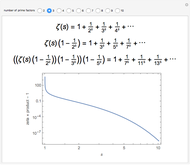
The Riemann zeta function is the analytic continuation of the function  , where
, where  ,
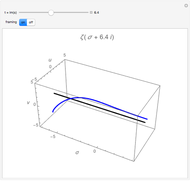
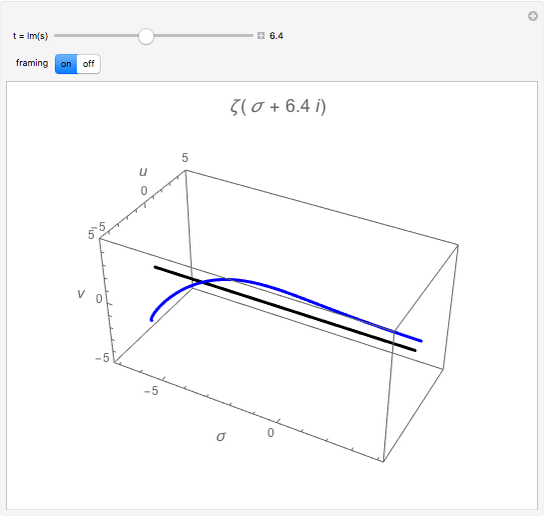
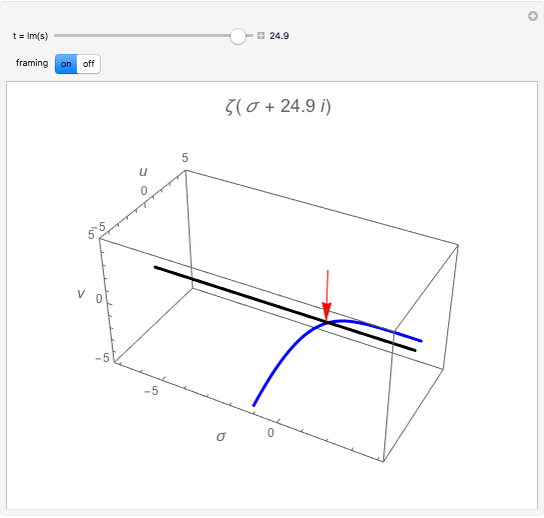
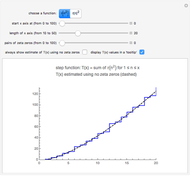
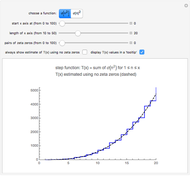
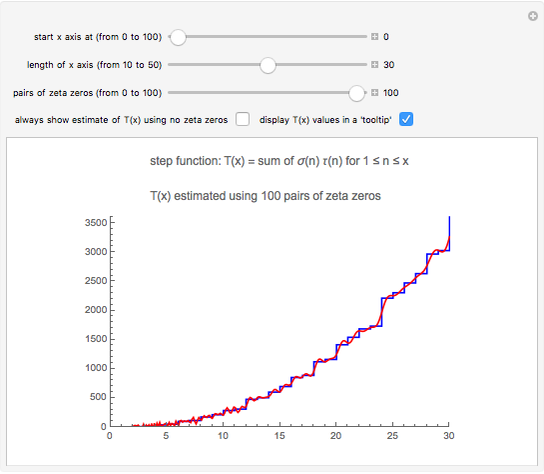
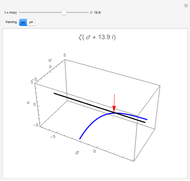
,  . The blue curve is a plot of
. The blue curve is a plot of  . You can vary
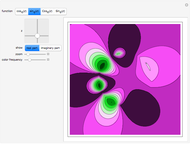
. You can vary  using the slider; it acts as the fourth dimension. The black line marks the origin of the
using the slider; it acts as the fourth dimension. The black line marks the origin of the  -
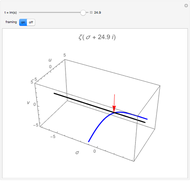
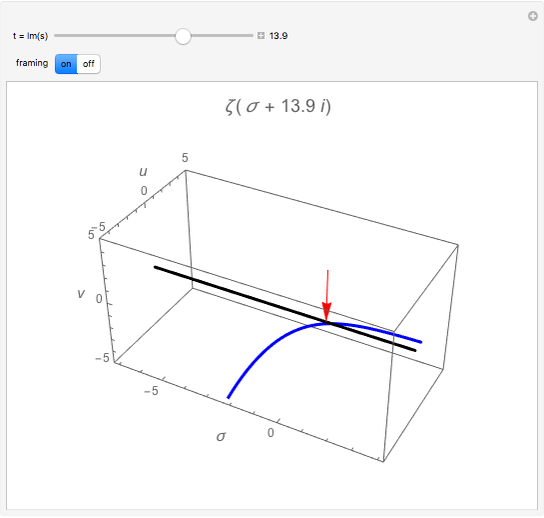
- complex plane. The red arrows mark where the zeta function (blue line) crosses the black line (
complex plane. The red arrows mark where the zeta function (blue line) crosses the black line ( ); these are some of the zeros of the zeta function. The so-called trivial zeros appear at negative even integers when
); these are some of the zeros of the zeta function. The so-called trivial zeros appear at negative even integers when  . The Riemann conjecture states that the nontrivial zeros all lie on the critical line
. The Riemann conjecture states that the nontrivial zeros all lie on the critical line  .
.
Contributed by: Biswaroop Mukherjee (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
See an English translation of [1].
Reference
[1] B. Riemann, "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse," Monatsberichte der Berliner Akademie in Gesammelte Werke, Teubner, Leipzig 1892. http://www.claymath.org/millennium-problems/riemann-hypothesis.
Permanent Citation
"The Riemann Zeta Function in Four Dimensions"
http://demonstrations.wolfram.com/TheRiemannZetaFunctionInFourDimensions/
Wolfram Demonstrations Project
Published: April 5 2011