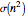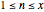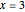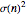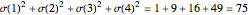Using Zeta Zeros to Compute Sigma Sums

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In number theory, the sum of the divisors of an integer  is usually denoted by
is usually denoted by 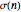 . (
. ( is the lowercase Greek letter sigma.) For example, 4 has three divisors (namely, 1, 2, and 4), so
is the lowercase Greek letter sigma.) For example, 4 has three divisors (namely, 1, 2, and 4), so 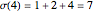 .
.
Contributed by: Robert Baillie (May 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
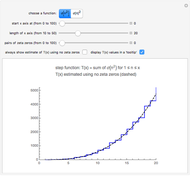
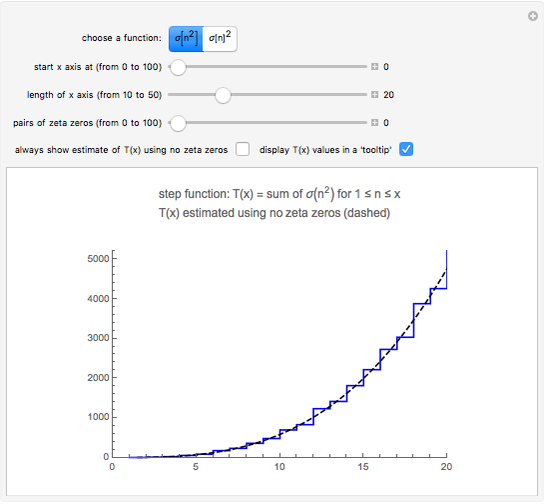
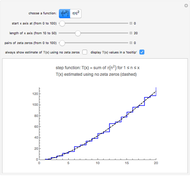
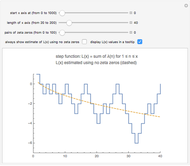
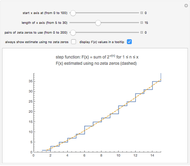
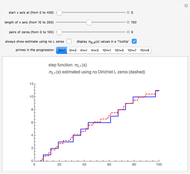
Snapshot 1: the graphs of the step function 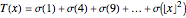 and the formula using no zeta zeros
and the formula using no zeta zeros
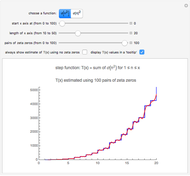
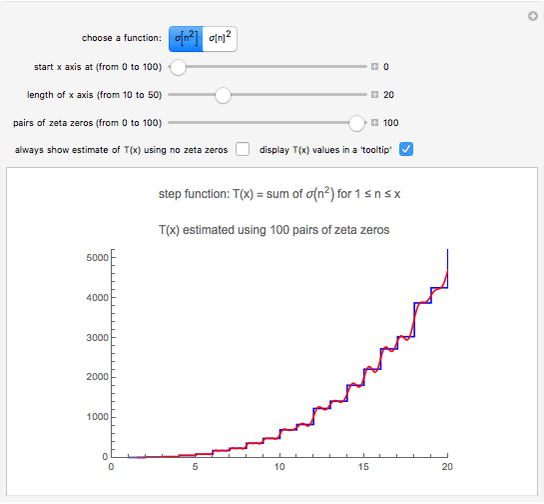
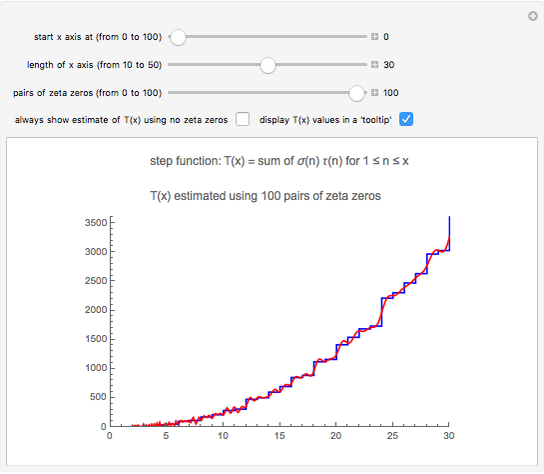
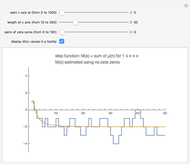
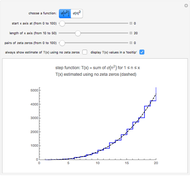
Snapshot 2: the graphs of  and the formula using 100 pairs of zeta zeros
and the formula using 100 pairs of zeta zeros
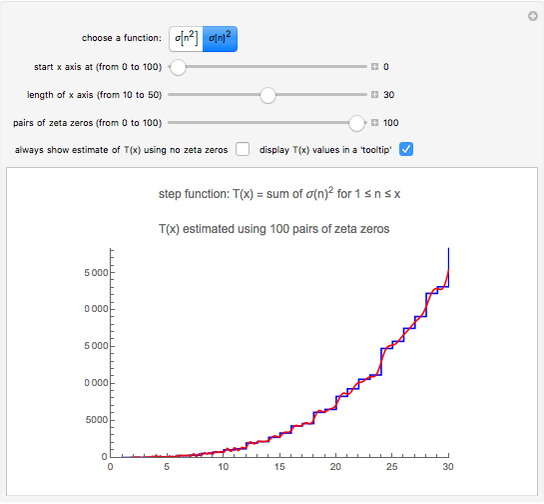
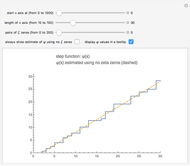
Snapshot 3: the graphs of 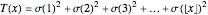 and the formula using 100 pairs of zeta zeros
and the formula using 100 pairs of zeta zeros
Here is the step function that is graphed when the left-hand button is pressed:
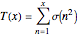 .
.
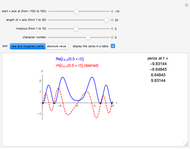
After you use the slider to choose 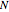 (the number of pairs of zeta zeros to use), this Demonstration uses the following formula to calculate
(the number of pairs of zeta zeros to use), this Demonstration uses the following formula to calculate  :
:
(1) 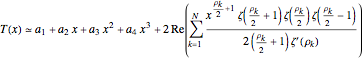 .
.
In this formula,
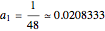 ,
,
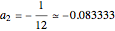 ,
,
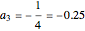 ,
,
and
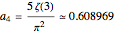 .
.
In equation (1),  is the
is the 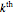 complex zero of the Riemann zeta function with positive real part. The first three complex zeros of the zeta function are approximately
complex zero of the Riemann zeta function with positive real part. The first three complex zeros of the zeta function are approximately 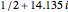 ,
, 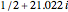 , and
, and 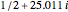 . These zeros occur in conjugate pairs, so if
. These zeros occur in conjugate pairs, so if 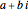 is a zero, then so is
is a zero, then so is 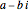 .
.
If you use the slider to choose, say, 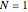 (one pair of zeta zeros), then the sum in equation (1) adds the two terms that correspond to the first pair of conjugate zeros,
(one pair of zeta zeros), then the sum in equation (1) adds the two terms that correspond to the first pair of conjugate zeros, 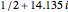 and
and 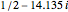 . These terms are conjugates of each other. When these terms are added, their imaginary parts cancel while their real parts add. So, the
. These terms are conjugates of each other. When these terms are added, their imaginary parts cancel while their real parts add. So, the 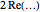 applied to the sum is merely an efficient way to combine the two terms for each pair of zeta zeros.
applied to the sum is merely an efficient way to combine the two terms for each pair of zeta zeros.
If you plot a graph using no zeta zeros, then the graph is computed with only the terms 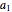 through
through 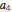 .
.
Now consider the step function that is graphed when the right-hand button is pressed:
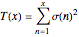 .
.
Here is the formula used to graph this function:
(2) 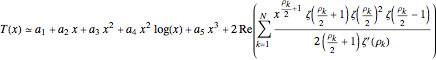
where
 ,
,
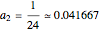 ,
,
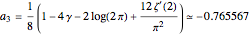 ,
,
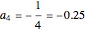 ,
,
and
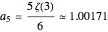
where 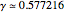 is Euler's constant.
is Euler's constant.
If you plot a graph using no zeta zeros, then the graph is computed with only the terms 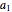 through
through  .
.
Where Do Equations (1) and (2) Come From?
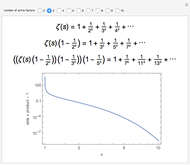
To prove equation (1), we start with the following identity, which holds for  (see [3], equation 5.39):
(see [3], equation 5.39):
(3) 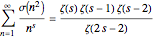 .
.
Perron's formula (see reference [4]) takes an identity like equation (3) and gives a formula for the sum of the numerators as a function of  , in this case,
, in this case, 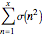 .
.
When we apply Perron's formula to equation (3), we get equation (1). To apply Perron's formula, we integrate this integrand
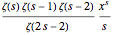
around a contour in the complex plane. Each part of equation (1) is the residue at one of the poles of this integrand. The residue at the pole at 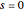 is
is 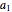 . At
. At  ,
,  has a pole (of order 1), so the integrand has poles of order 1 at
has a pole (of order 1), so the integrand has poles of order 1 at  , at
, at 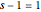 , and at
, and at  . The residue at the pole
. The residue at the pole 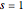 is
is 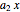 . The residue at
. The residue at  is
is  . The residue at
. The residue at  is
is 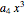 .
.
Mathematica can compute these residues. For example, this calculation Residue[Zeta[s] Zeta[s-1] Zeta[s-2]/Zeta[2 s-2] x^s/s,{s,3}] gives 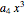 , where
, where 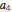 has the value given above for equation (1).
has the value given above for equation (1).
Finally, the integrand has a pole at each complex zero of 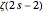 . The first sum in equation (1) is just the sum of the residues at these complex zeros of zeta. Each complex zero gives rise to one term in the sum. (The
. The first sum in equation (1) is just the sum of the residues at these complex zeros of zeta. Each complex zero gives rise to one term in the sum. (The 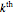 complex zero of
complex zero of 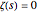 is
is 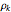 , so
, so 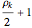 is the
is the 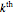 complex zero of
complex zero of 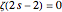 .)
.)
The integrand also has poles at the real zeros of 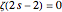 (i.e., at
(i.e., at 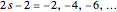 , in other words, at
, in other words, at 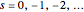 ). However, all these residues are 0 except at
). However, all these residues are 0 except at 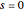 , where the residue is
, where the residue is 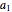 .
.
Equation (2) is proved the same way. We start with this identity, which holds for 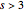 (see [1], equation D-58, and [2], Theorem 305):
(see [1], equation D-58, and [2], Theorem 305):
 .
.
As with equation (1), we apply Perron's formula, this time using the integrand
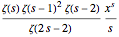 .
.
The Demonstration "Using Zeta Zeros to Tally Squarefree Divisors" gives additional details on Perron's formula.
References
[1] H. W. Gould and T. Shonhiwa, "A Catalog of Interesting Dirichlet Series".
[2] G. H. Hardy and E. M. Wright, An Introduction to the Theory of Numbers, 4th ed., Oxford: Oxford University Press, 1965, p. 256.
[3] P. J. McCarthy, Introduction to Arithmetical Functions, New York: Springer-Verlag, 1986, p. 237.
[4] H. L. Montgomery and R. C. Vaughan, Multiplicative Number Theory: I. Classical Theory, Cambridge: Cambridge University Press, 2007, p. 397.
Permanent Citation