The Sum of the Squares of the Distances to N Points

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
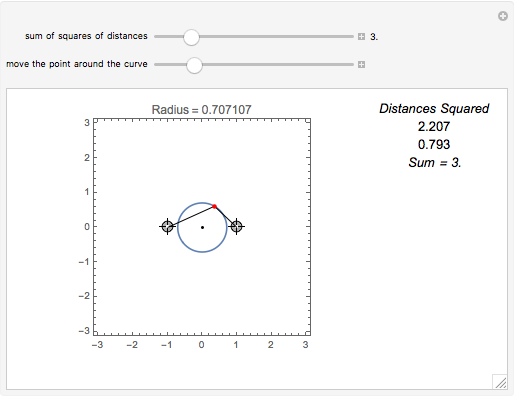
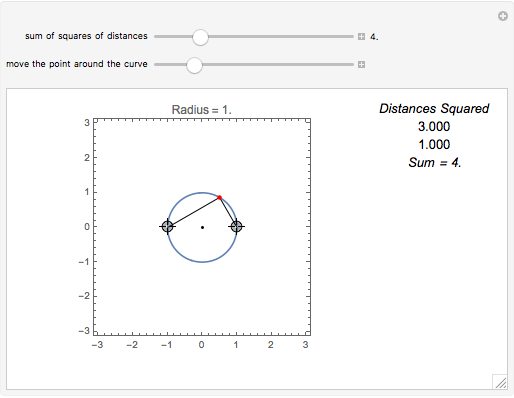
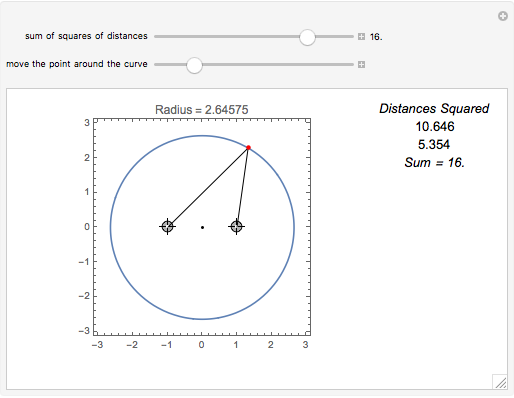
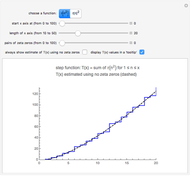
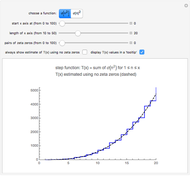
A circle is the locus of points that are a given distance from a given point. An ellipse is the locus of points such that the sum of the distances to two fixed points is constant. What is the locus of points such that the sum of the squares of the distances to two fixed points is constant?
Contributed by: Robert Baillie (July 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
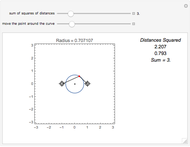
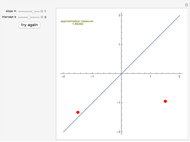
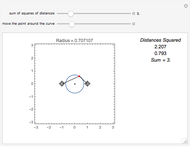
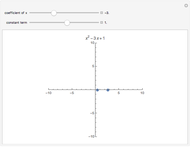
Snapshot 1: the sum of the squares of the distances to two fixed points (-1, 0) and (1, 0) equals 3
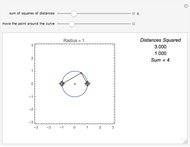
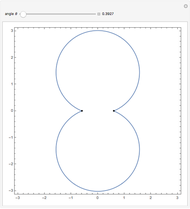
Snapshot 2: the sum of the squares of the distances to two fixed points (-1, 0) and (1, 0) equals 4
Snapshot 3: the sum of the squares of the distances to two fixed points (-1, 0) and (1, 0) equals 16
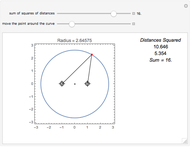
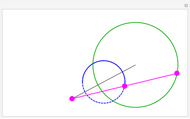
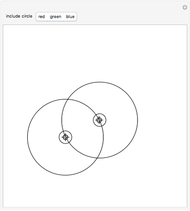
Snapshot 4: the sum of the squares of the distances to three fixed points (-1, 0), (1, 0), and (2, -1) equals 16
We often define a circle as the locus of points that are a given distance from a given point. The given distance is the radius, and the given point is the center.
Likewise, an ellipse is often defined as the locus of points such that the sum of the distances to two fixed points is constant. The two fixed points are the foci.
Suppose we tweak these definitions and ask, "What is the locus of points such that the sum of the squares of the distances to two fixed points is constant?"
Assuming the sum is large enough, the locus is a circle.
We can generalize this: if 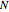 is any positive integer, a circle is the locus of points such that the sum of the squares of the distances to
is any positive integer, a circle is the locus of points such that the sum of the squares of the distances to 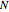 fixed points is constant (again, provided the sum is large enough).
fixed points is constant (again, provided the sum is large enough).
Here is the proof for the case  . Write the equation for the sum of the squares of the distances to the two points
. Write the equation for the sum of the squares of the distances to the two points 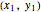 and
and 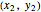 :
:
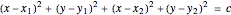 .
.
Expand, then rearrange the equation, then divide through by 2 to get this:
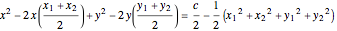 . (1)
. (1)
Notice that 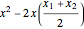 are the first two terms of
are the first two terms of 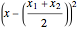 . We can convert
. We can convert 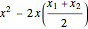 into a square by adding
into a square by adding 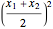 to both sides of equation (1). This is called "completing the square". When we do this for both the
to both sides of equation (1). This is called "completing the square". When we do this for both the  and
and 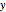 terms, we get the equation for a circle:
terms, we get the equation for a circle:
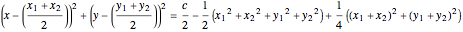 . (2)
. (2)
The center of the circle is at the point
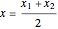 ,
, 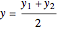 .
.
If the right-hand side of equation (2) is a number greater than 0, then the radius is the square root of that number.
You can use Alt+Click to add more locators or to delete existing ones.
This also generalizes to higher dimensions. For example, in 3-space, a sphere is the locus of points such that the sum of the squares of the distances to 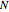 fixed points is constant.
fixed points is constant.
Permanent Citation