Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

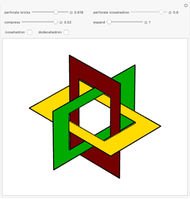
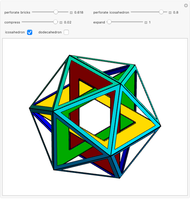
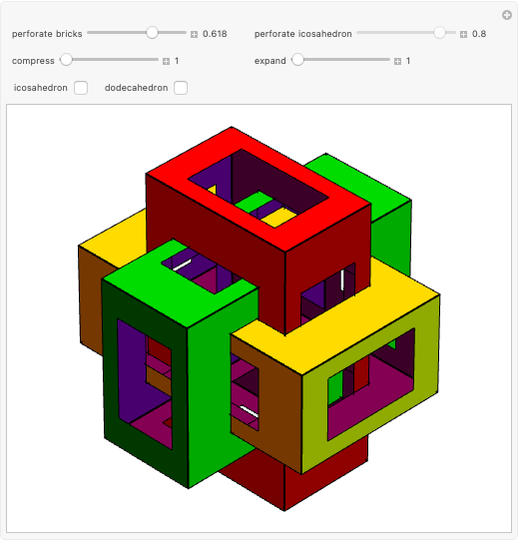
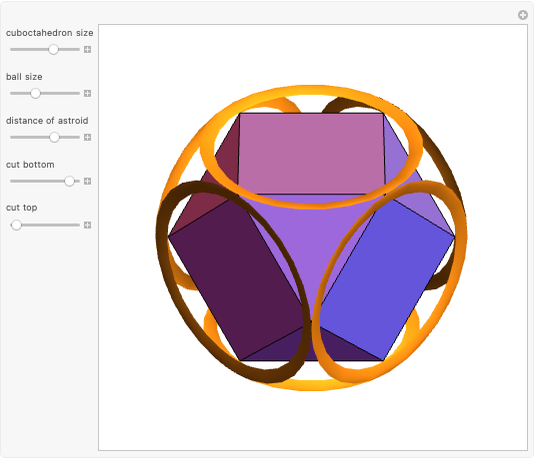
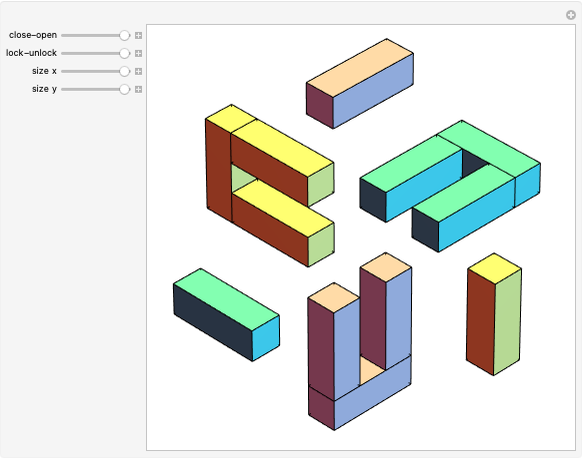
Three Interpenetrating Golden Bricks

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

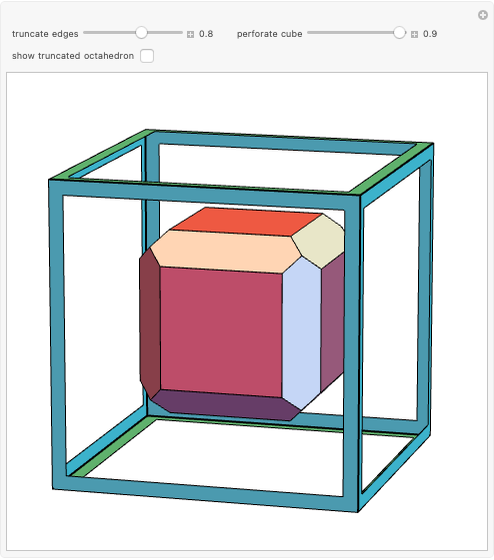
Each of three mutually perpendicular bricks have sides 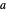, , such that 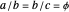, where is the golden ratio. Each face is perforated again with sides in the proportion of the golden ratio.

[more]

The bricks are fit tightly together as a Borromean ring. When they are compressed, the vertices of the resulting golden rectangles coincide with the vertices of an icosahedron. When the golden rectangles are extended until equal to the square of the golden ratio, the edges coincide with the edges of a dodecahedron.

[less]

Contributed by: Sándor Kabai (January 2023)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send