Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

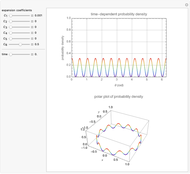
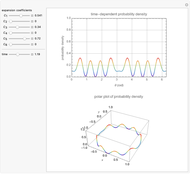
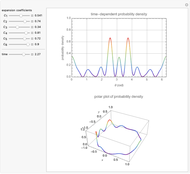
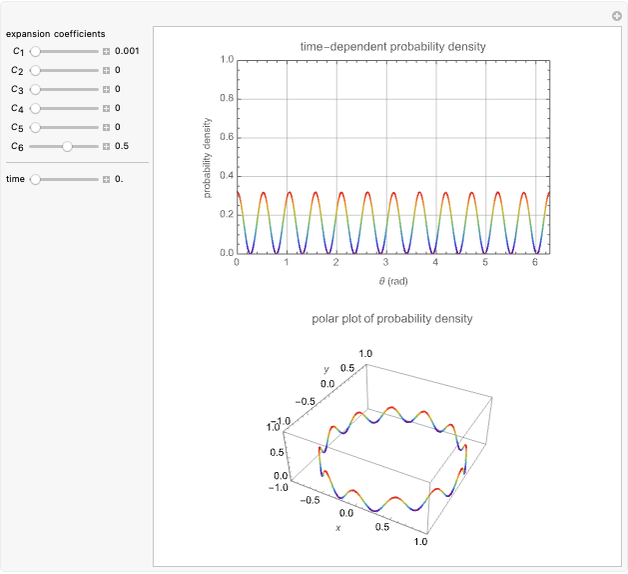
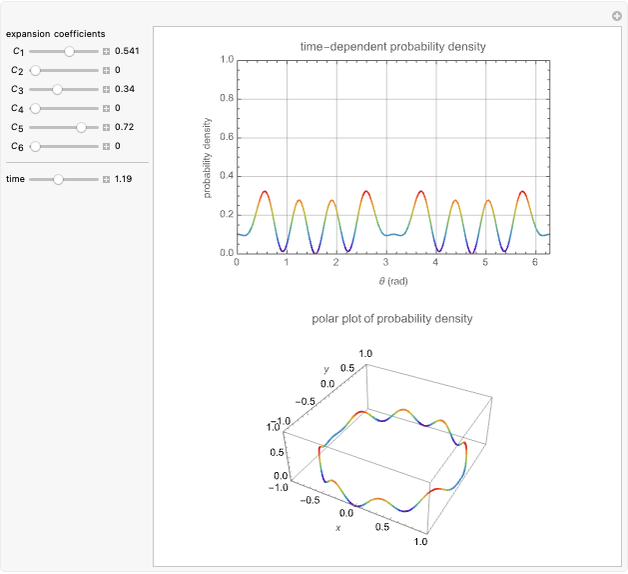
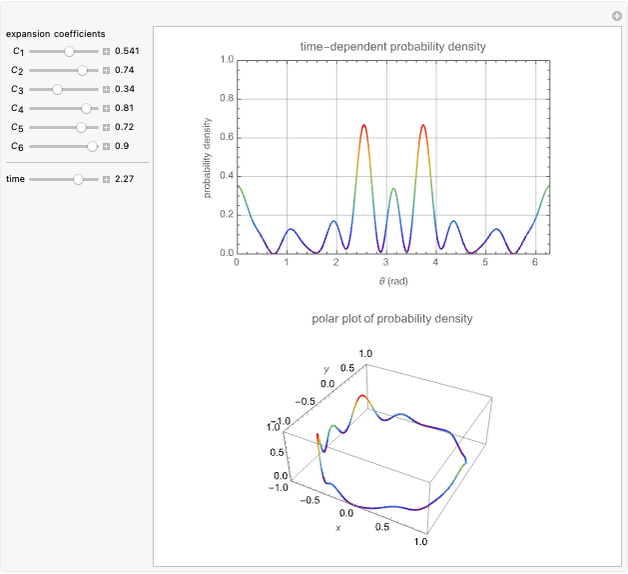
Time-Dependent Probability Density of Nonstationary States of an Electron in a Ring

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

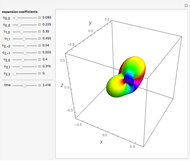
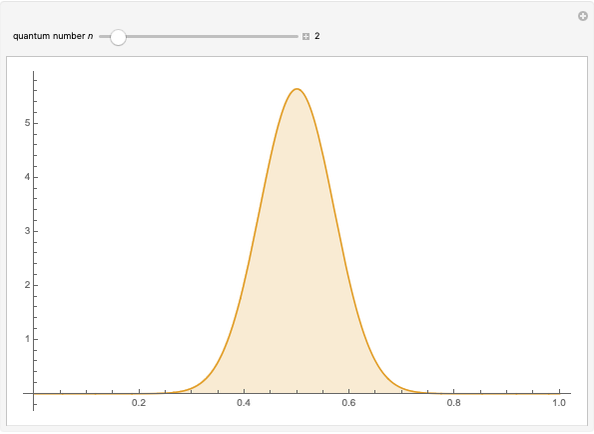
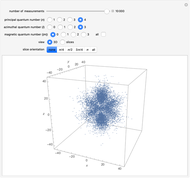
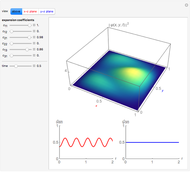
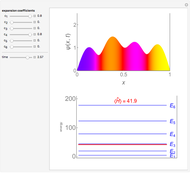
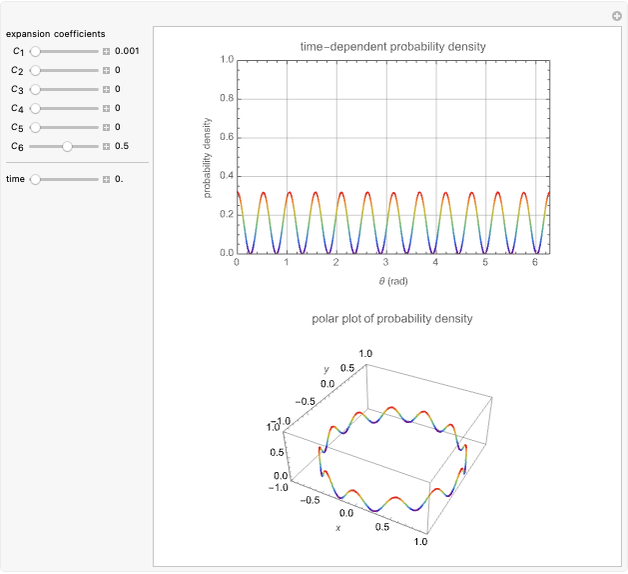
This Demonstration considers the probability density of nonstationary states of an electron of mass in a ring of radius . The wavefunction is given by

[more]

,

which is a superposition of eigenstates, with and . The upper plot shows the probability density as a function of the angle (in radians). The lower diagram shows a polar plot of the probability density of the electron around the ring as a function of time . The color changes with the probability density, red indicating the highest density, and blue, the lowest.

[less]

Contributed by: Valerie Greenwood, Rachel Kallianis and Anne Huetteman (May 8)
Open content licensed under CC BY-NC-SA

Details

References

[1] S. Montenegro and S. M. Blinder, "Particle on a Ring," LibreTexts Chemistry (Apr 11, 2023) chem.libretexts.org/Bookshelves/Physical_and_Theoretical _Chemistry _Textbook _Maps/Supplemental_Modules_ (Physical_and _Theoretical _Chemistry)/Quantum_Mechanics/05.5%3 A_Particle _in _Boxes/Particle_on_a _Ring.

[2] B. D. Anderson, "Cyclic Polyynes as Examples of the Quantum Mechanical Particle on a Ring," Journal of Chemical Education, 89(6), 2012 pp. 724–727. doi:10.1021/ed200439u.

[3] S. Stuart, Particle on a Ring [Video], YouTube. (Apr 11, 2023) www.youtube.com/watch?v=HOhhTfdDZt8.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send