Electron Probability Distribution for the Hydrogen Atom

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
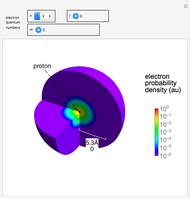
The electron in a hydrogen atom is described by the Schrödinger equation. The time-independent Schrödinger equation in spherical polar coordinates 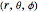 can be solved by separation of variables in the form
can be solved by separation of variables in the form  . The radial and angular components are Laguerre and Legendre functions, thus
. The radial and angular components are Laguerre and Legendre functions, thus 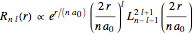 and
and  , respectively. Here,
, respectively. Here,  is the first Bohr radius, and
is the first Bohr radius, and  are the integers in the ranges
are the integers in the ranges 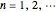 (principal quantum number),
(principal quantum number),  (angular momentum quantum number), and
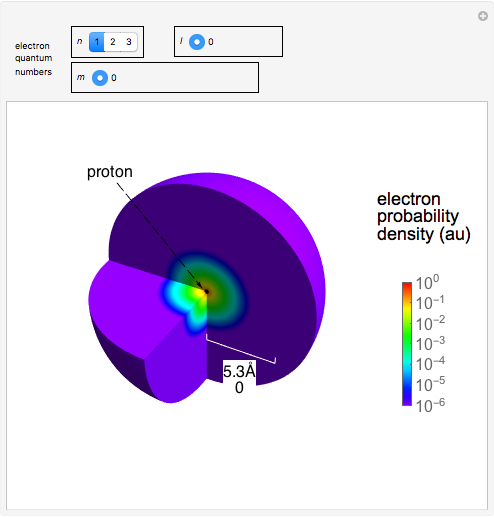
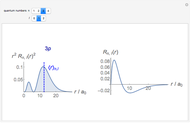
(angular momentum quantum number), and  (magnetic quantum number). The probability of finding an electron at a specific location is given by
(magnetic quantum number). The probability of finding an electron at a specific location is given by  , where
, where  is the normalization constant, such that
is the normalization constant, such that  .
.
Contributed by: Y. Shibuya (April 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
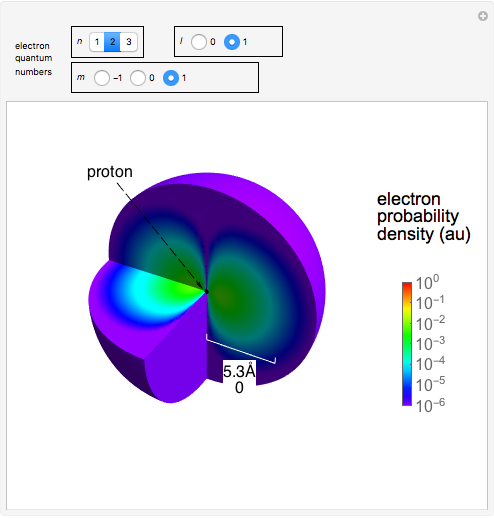
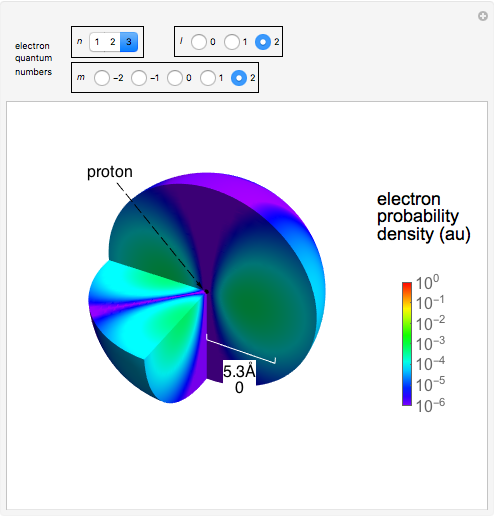
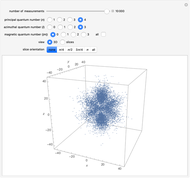
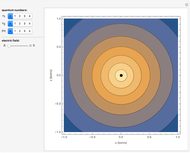
The electron is confined to a space of the order of a few angstroms for  . For
. For  , the space expands beyond the display limit (
, the space expands beyond the display limit ( in radius). The patterns for positive and negative
in radius). The patterns for positive and negative  values are the same since only the real part of
values are the same since only the real part of  is shown.
is shown.
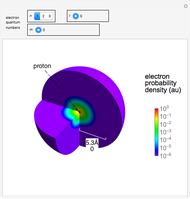
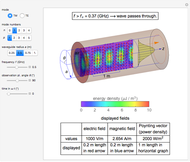
Snapshot 1: distribution for  ,
, 
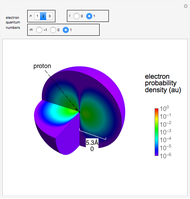
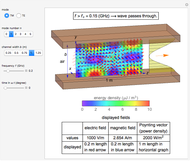
Snapshot 2: distribution for  ,
, 
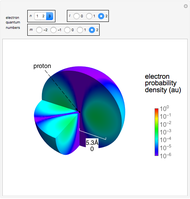
Snapshot 3: distribution for  ,
, 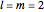
Reference
[1] J. C. Slater, Modern Physics, New York: McGraw-Hill, 1955.
Permanent Citation