Torsion of an Elastic Beam with Rectangular Cross Section

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
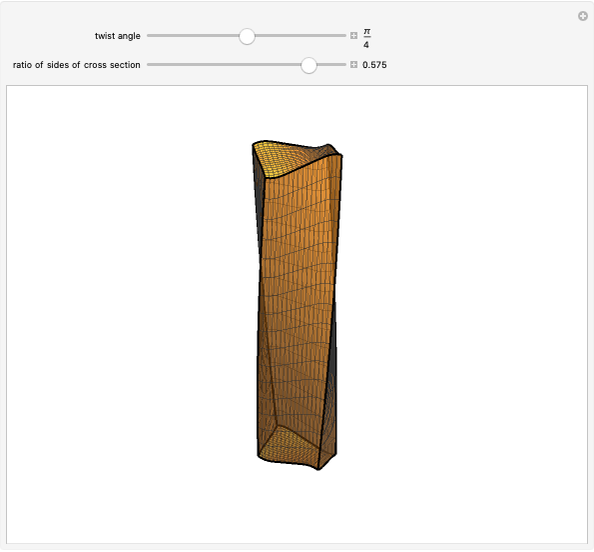
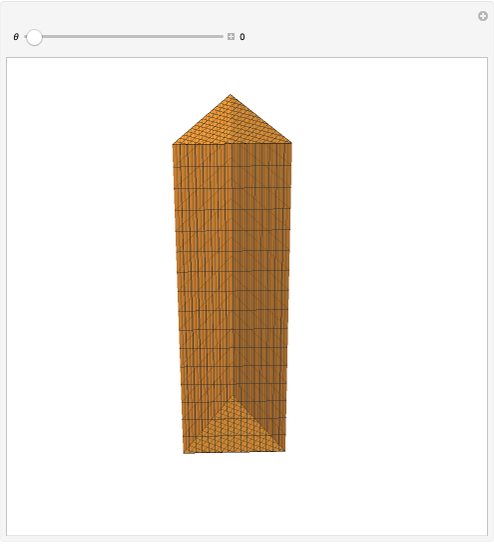
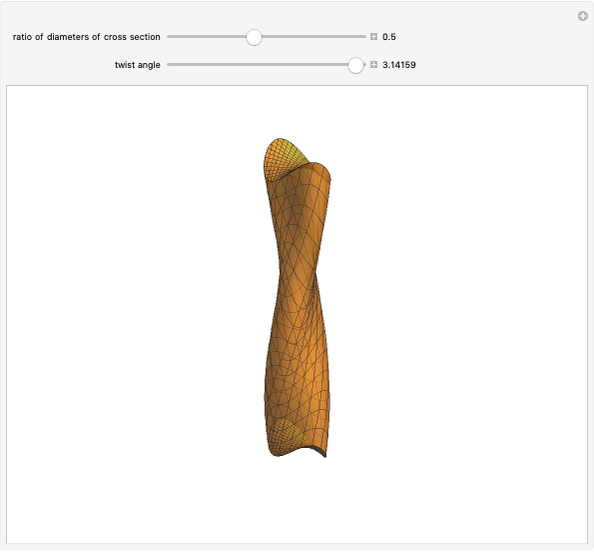
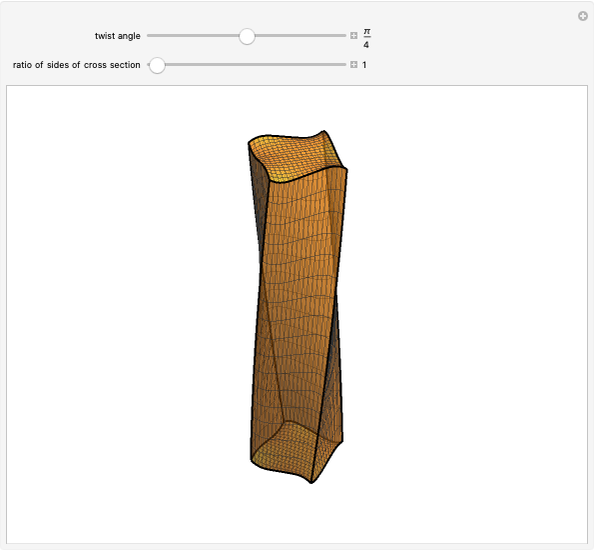
This Demonstration shows in 3D the analytic solution of the torsion of a prism with rectangular cross section as presented in [1].
Contributed by: Maurizio Brocato (February 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
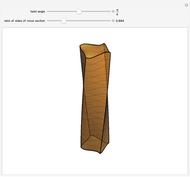
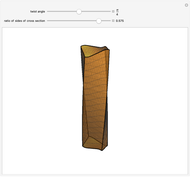
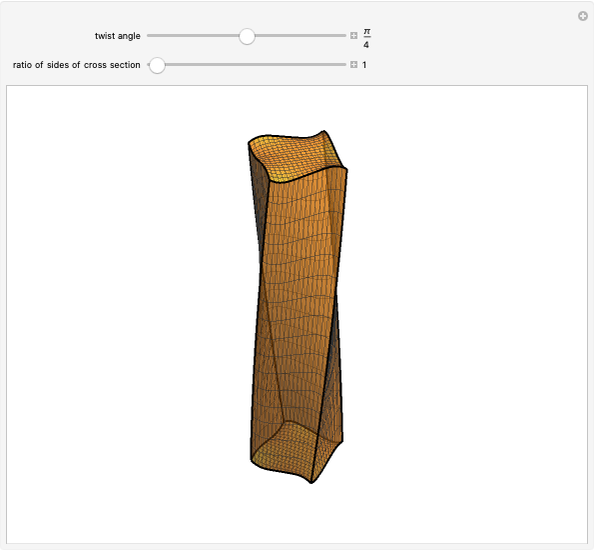
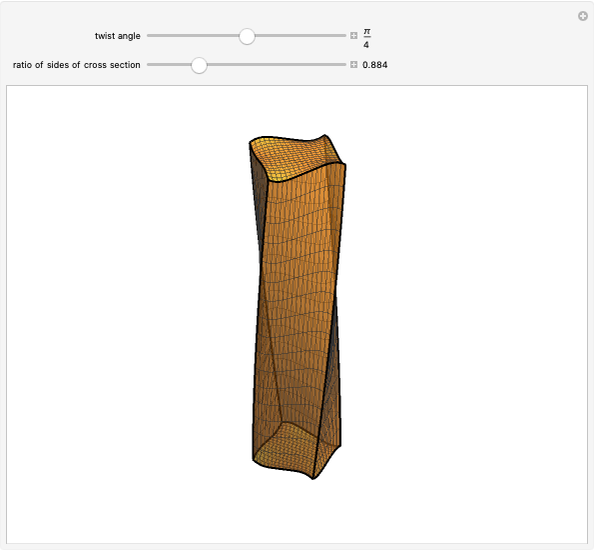
The animation represents the solution of the torsion problem for an elastic beam with square cross section. The solution is given in [1] under the classical assumptions of the standard theory of beams, i.e. prismatic geometry, linear elastic homogeneous isotropic material, small deformations and small displacements, unloaded lateral surface. The loading conditions are defined according to the so-called Saint-Venant problem: only the resultant force and moment on the end bases are given and respect the overall equilibrium conditions.
Details are given in textbooks on the theory of elasticity or on structural mechanics including elements of the theory of elastic beams. For example, see [2].
The computed shape of the end bases is the so-called warping function, which depends uniquely on the shape of the cross section of the beam and is the solution of a particular Neumann problem (null Laplacian on the whole surface and normal derivative on the boundary).
References
[1] A.-J.-C. Barré de Saint-Venant, De la torsion des prismes avec des considérations sur la flexion ainsi que sur l’équilibre des solides élastiques [...], Paris: Imprimerie Impériale, 1855.
[2] M. Brocato, Cours de mécanique des structures. Volume 1. Poutres élastiques, Paris: Presses des Ponts, forthcoming.
Permanent Citation